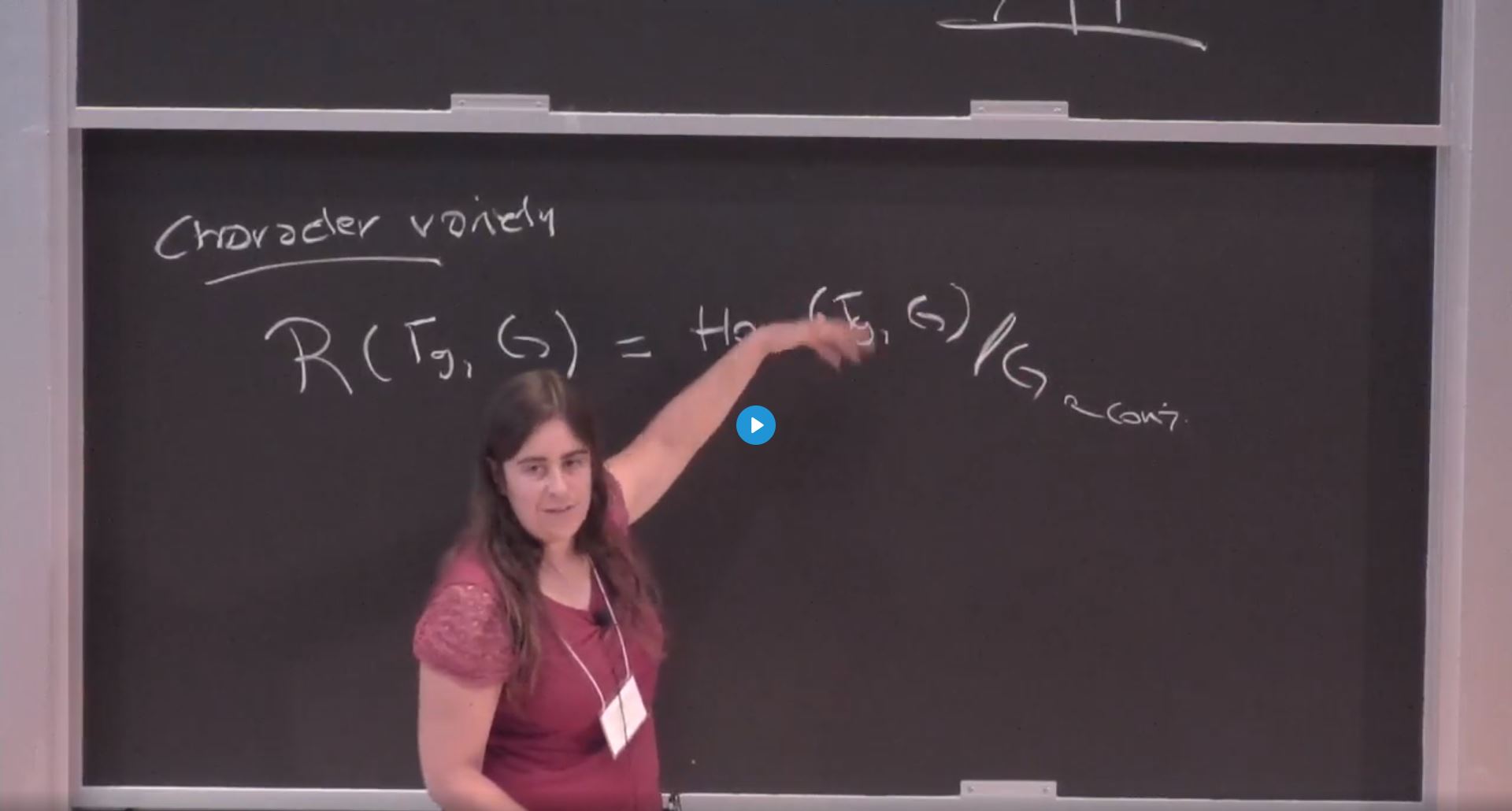Maximal representations form unexpected connected components of the character variety of the fundamental group of a hyperbolic surface in a semisimple Lie group, that only consist of injective homomorphsims with discrete image. They thus generalize the Teichmüller space, and can be thought of as parametrizing certain locally symmetric spaces of infinite volume. After a general introduction to character varieties and maximal representations, I will discuss joint work with Andres Sambarino and Anna Wienhard in which we prove a sharp upper bound for the exponential orbit growth rate of the associated actions on the symmetric space.