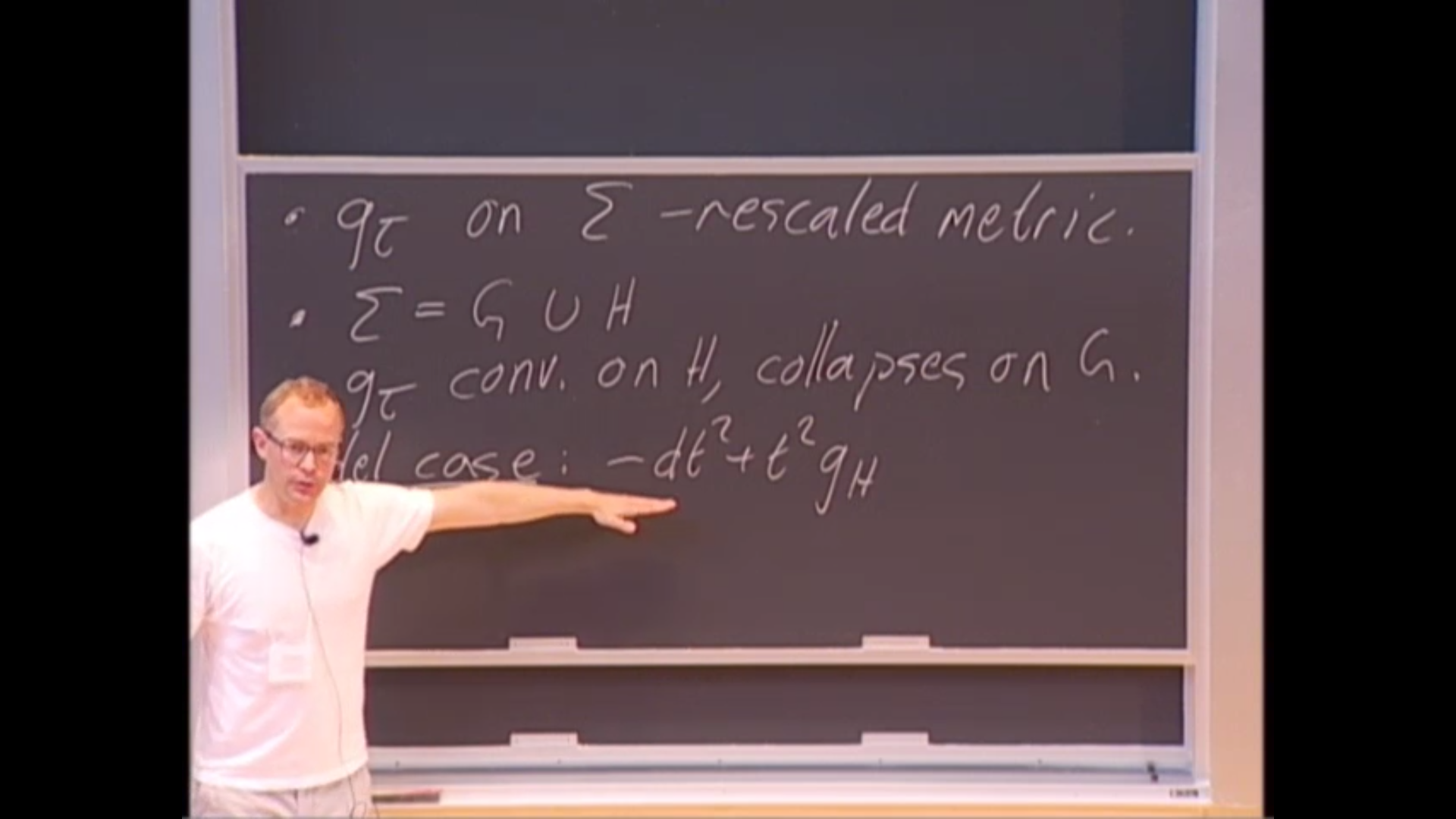Solutions to Einstein's equations with a high degree of symmetry play an important role in guiding our understanding of general relativity. It is therefore natural to ask: to what extent are these solutions representative? In the talk we give examples both of stability and instability and relate the results to more general conjectures. In particular, we illustrate the strong dependence of the conclusions on the presence/absence of a positive cosmological constant.