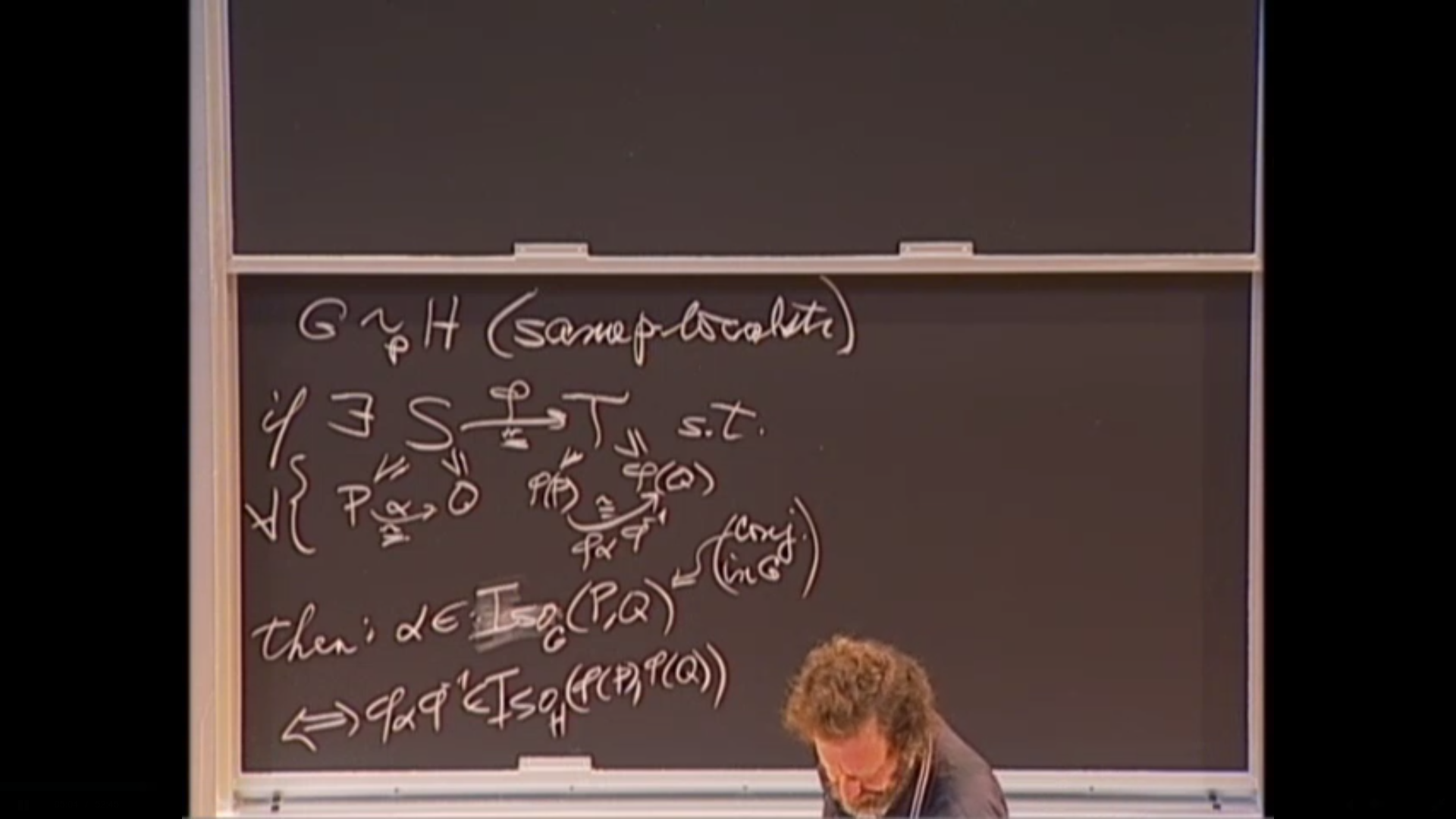Local structure of groups and of their classifying spaces
Presenter
January 30, 2014
Keywords:
- p-local structure
- Martino-Priddy conjecture
- fusion system
- fusion category
- classifying space
- discrete p-toral group
MSC:
- 55R40
- 55R35
- 55Rxx
- 22E35
- 22Exx
- 22E05
- 22Exx
Abstract
This will be a survey talk on the close relationship between the local structure of a
nite group or compact Lie group and that of its classifying space. By the p-local structure of a group G, for a prime p, is meant the structure of a Sylow p-subgroup S G (a maximal p-toral subgroup if G is compact Lie), together with all G-conjugacy relations between elements and subgroups of S. By the p-local structure of the classifying space BG is meant the structure (homotopy properties) of its p-completion BG^p . For example, by a conjecture of Martino and Priddy, now a theorem, two
nite groups G and H have equivalent p-local structures if and only if BG^p ' BH^p . This was used, in joint work with Broto and Møller, to prove a general theorem about local equivalences between
nite Lie groups a result for which no purely algebraic proof is known. As another example, these ideas have allowed us to extend the family of p-completed classifying spaces of (
nite or compact Lie) groups to a much larger family of spaces which have many of the same very nice homotopy theoretic properties.