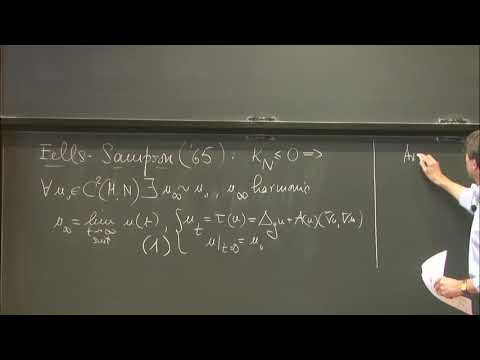Abstract: Finding non-constant harmonic 3-spheres for a closed target manifold N is a prototype of a super-critical variational problem. In fact, the direct method fails, as the infimum of the Dirichlet energy in any homotopy class of maps from the 3-sphere to any closed N is zero; moreover, the harmonic map heat flow may blow up in finite time, and even the identity map from the 3-sphere to itself is not stable under this flow. To overcome these difficulties, we propose the normalized harmonic map flow as a new tool, and we show that for this flow the identity map from the 3-sphere to itself now, indeed, is stable; moreover, the flow converges to a harmonic 3-sphere also when we perturb the target geometry. While our results are strongest in the perturbative setting, we also outline a possible global theory.