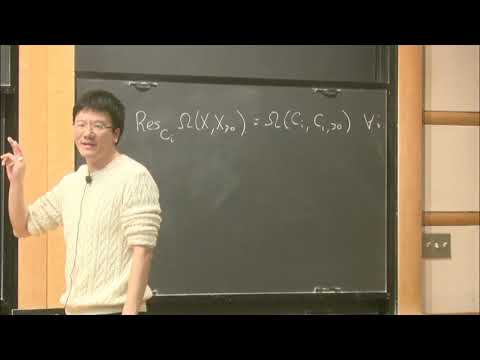Abstract
Positive geometries are real semialgebraic sets inside complex varieties characterized by the existence of a meromorphic top-form called the canonical form. The defining property of positive geometries and their canonical forms is that the residue structure of the canonical form matches the boundary structure of the positive geometry. A key example of a positive geometry is a projective polytope. I will discuss definitions and examples of positive geometries, and explain some applications of the canonical form. The talk is based on joint work with Arkani-Hamed and Bai, and with Galashin and Karp.