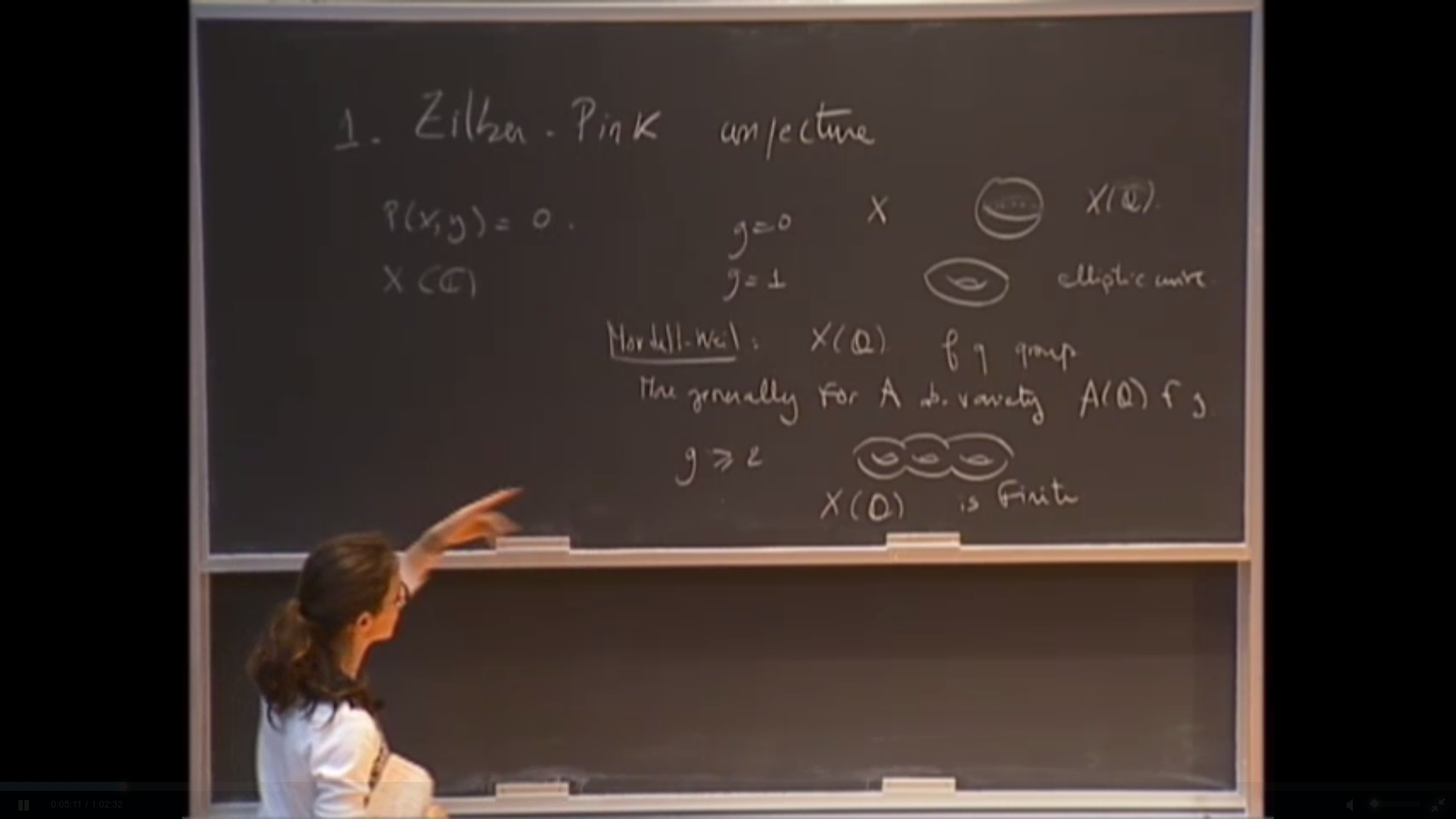Lehmer problem and applications
Presenter
February 10, 2014
Keywords:
- rational points on elliptic curves
- rational points on higher genus curves
- arithmetic geometry
- Diophantine geometry
- Mordell-Lang conjecture
- Zilber-Pink conjecture
MSC:
- 11Gxx
- 11G10
- 11G15
- 11G50
- 11G45
Abstract
Lehmer conjecture predicts a lower bound for the height of a non zero algebraic integer wich is not a root of unity in terms of its degree. In this talk, we explain how the relative Lehmer problem is related to the Zilber-Pink conjecture. The idea comes from the
rst article of Bombieri, Masser and Zannier on the subject : they used the lower bounds for the height given by the Lehmer problem to proove that the bounded height subset of Gn m that they were interested in, was
nite. Indeed, Lehmer type bounds are used to proove that such a subset has bounded degree and by Northcott property they conlcuded
niteness. We'll explain how this argument works in the context of abelian varieties.