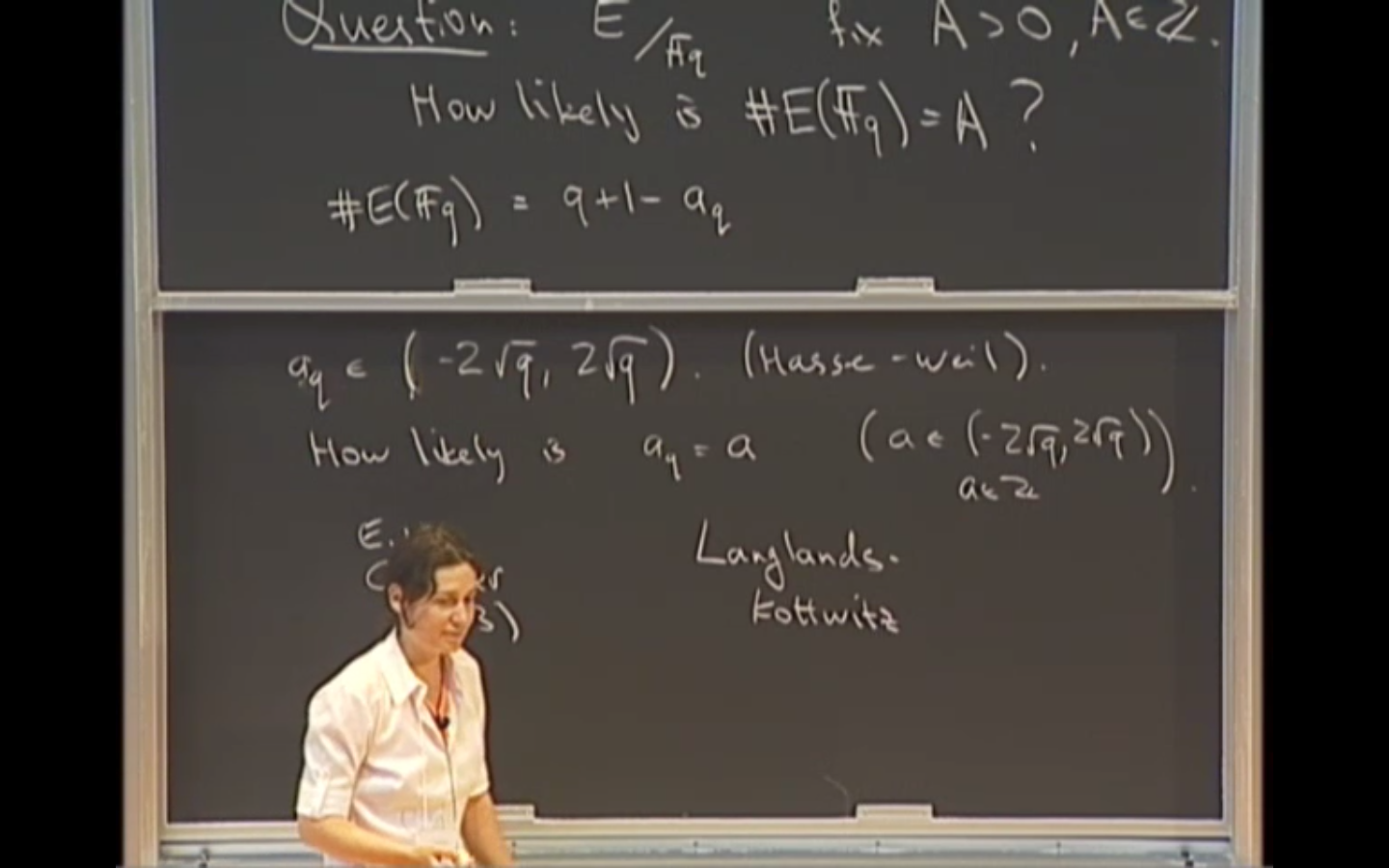Consider the question: how likely is a random elliptic curve over the finite field F_p to have exactly N rational points, where N is a given integer in the appropriate range? In 2003, Gekeler gave an explicit answer based on a heuristic that was too strong to be literally true, thus the answer appeared somewhat mysterious. We provide an explanation for this formula by making an explicit and very natural connection with a formula of Langlands and Kottwitz which expresses the size of an isogeny class of principally polarized abelian varieties in terms of an adelic orbital integral. Then we discuss a possible extension of Gekeler's computations from elliptic curves to abelian varieties.