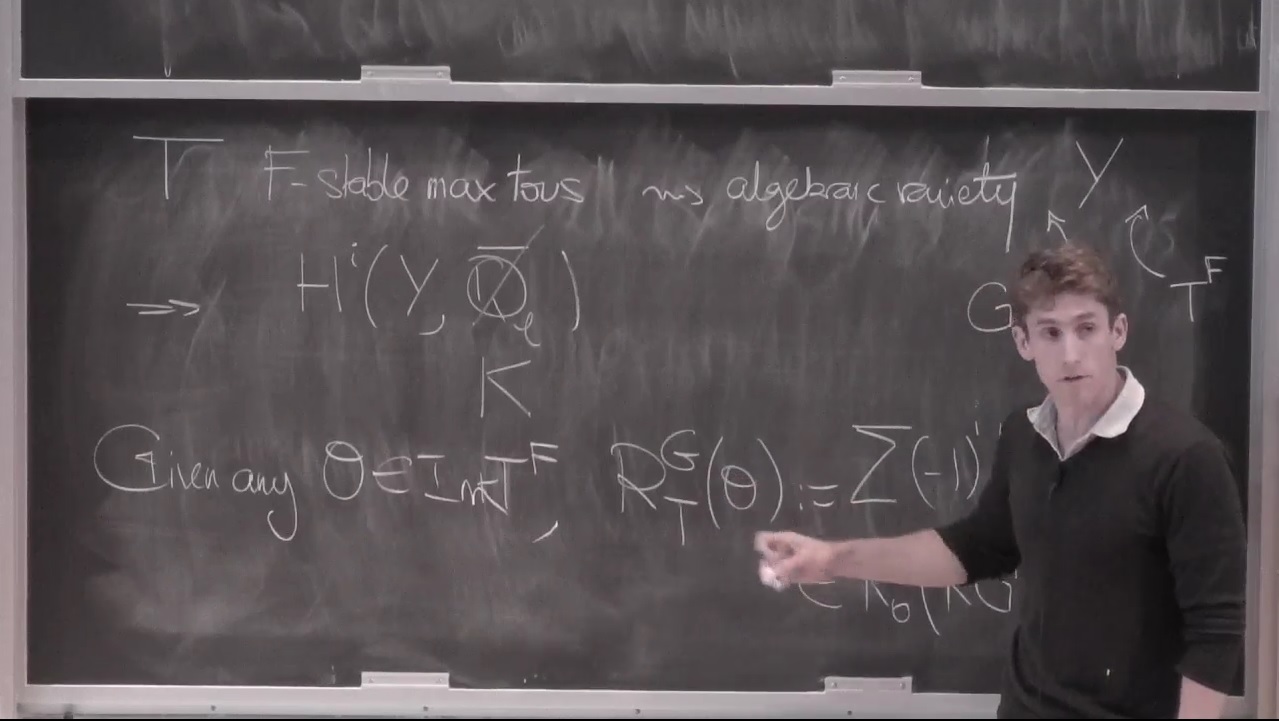This series of lectures will be centered on decomposition numbers for a special class of finite groups such as GL_n(q), SO_n(q),... E_8(q). I will first present what kind of numerical invariants decomposition numbers are, and what representation-theoretic problems they can solve. For finite reductive groups, I will explain how one can use Deligne--Lusztig theory to get basic sets of ordinary characters and to compute decomposition numbers. If time permits, I will mention a few open problems, including the case of small characteristic. Lecture 2 - Basic sets for finite reductive groups