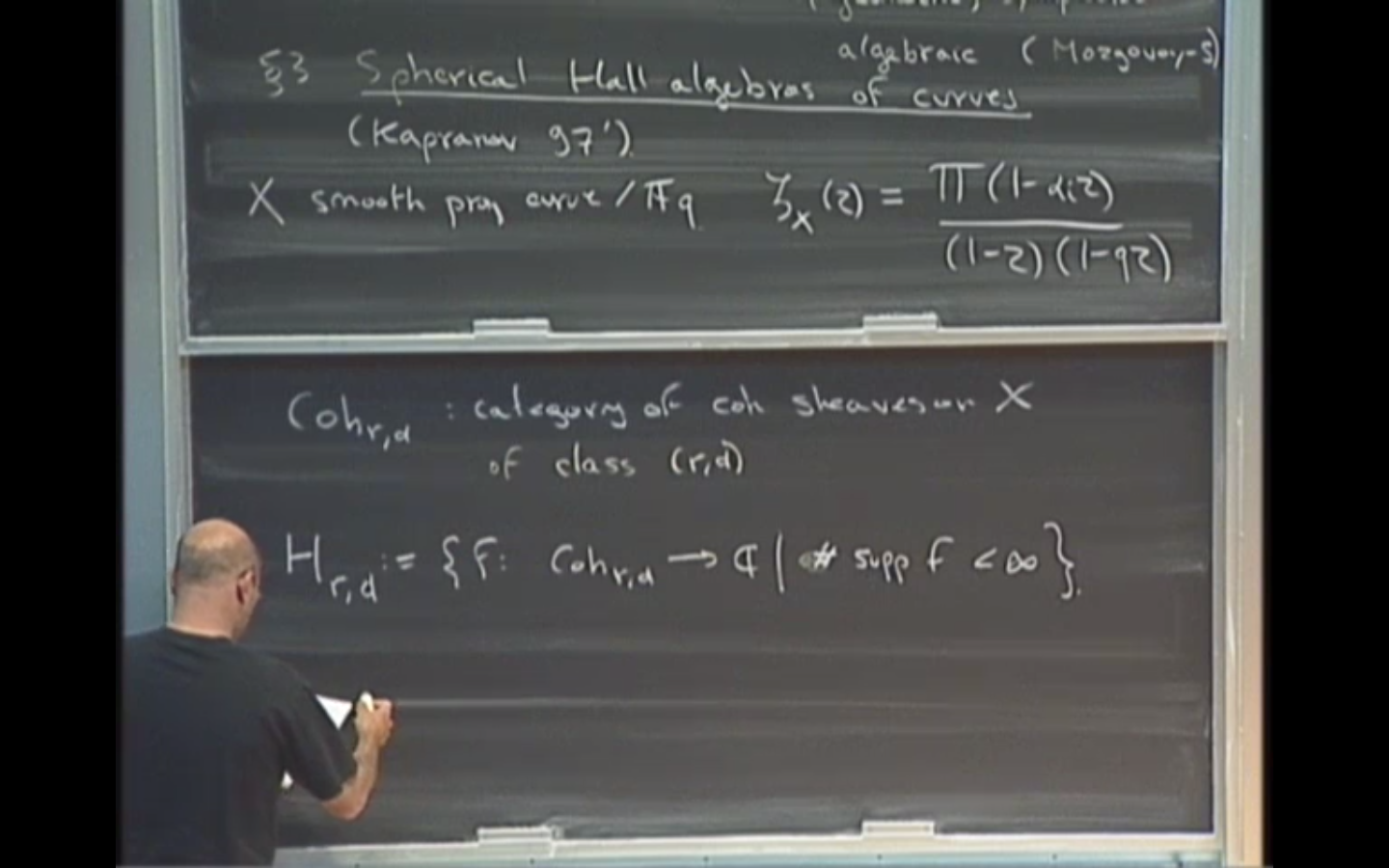In the early 80's Kac proved that the number of indecomposable representations of a given quiver (and a given dimension) over a finite field is a polynomial in the size of the finite field. Hua later gave an explicit formula for these polynomials and subsequent representation-theoretic or geometric interpretations for these polynomials were given by Crawley-Boevey, Van den Bergh, Hausel and others, leading to a beautiful and still mysterious picture. The aim of this mini-course is to explain a 'global' analog of some of these results, in which the category of representations of a quiver gets replaced by the category of coherent sheaves on a smooth projective curve. As an application, we will give a formula for the number of stable Higgs bundles over such a curve defined over a finite field.