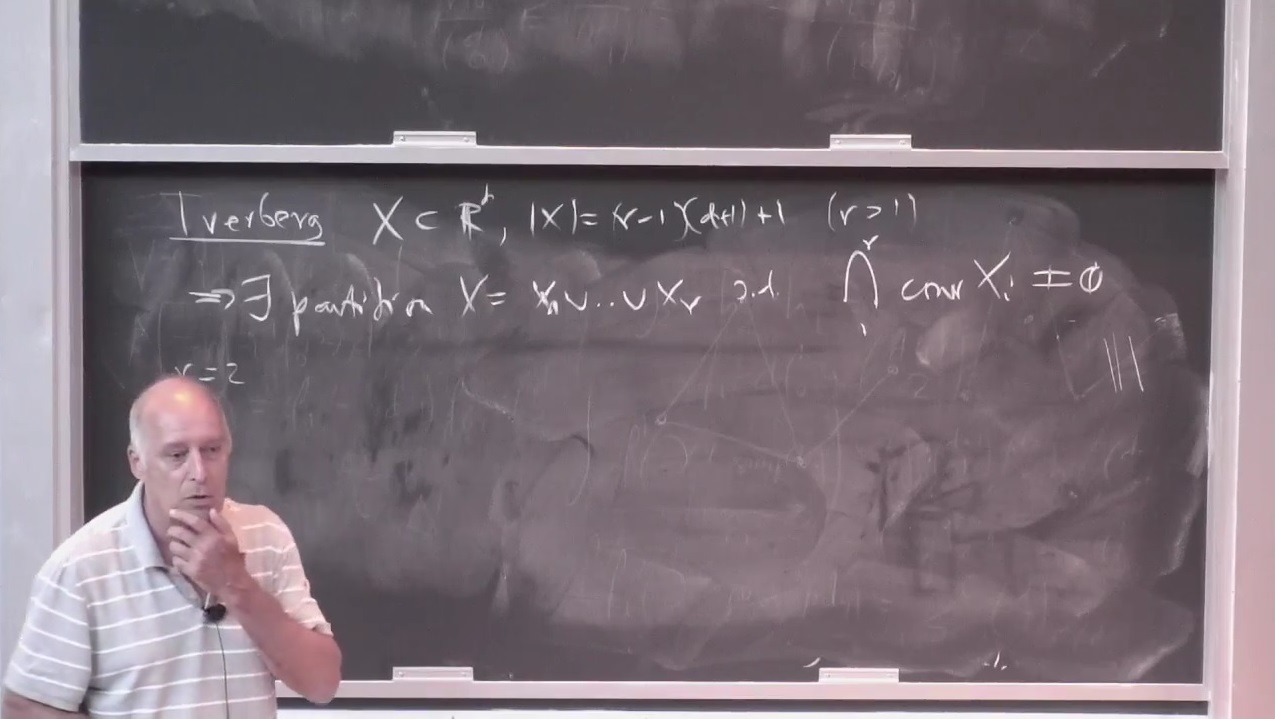Tverberg plus minus
Presenter
September 1, 2017
Keywords:
- Tverberg's theorem
- sign conditions
MSC:
- 52A35
- 52C45
Abstract
We prove a Tverberg type theorem: Given a set $A \subset \R^d$ in general position with $|A|=(r-1)(d+1)+1$ and $k\in \{0,1,\ldots,r-1\}$, there is a partition of $A$ into $r$ sets $A_1,\ldots,A_r$ (where $|A_p|\le d+1$ for each $p$) with the following property. The unique $z \in \bigcap_{p=1}^r \aff A_p$ can be written as an affine combination of the elements in $A_p$: $z=\sum_{x\in A_p}\al(x)x$ for every $p$ and exactly $k$ of the coefficients $\al(x)$ are negative. The case $k=0$ is Tverberg's classical theorem. This is joint works with Pablo Soberon.