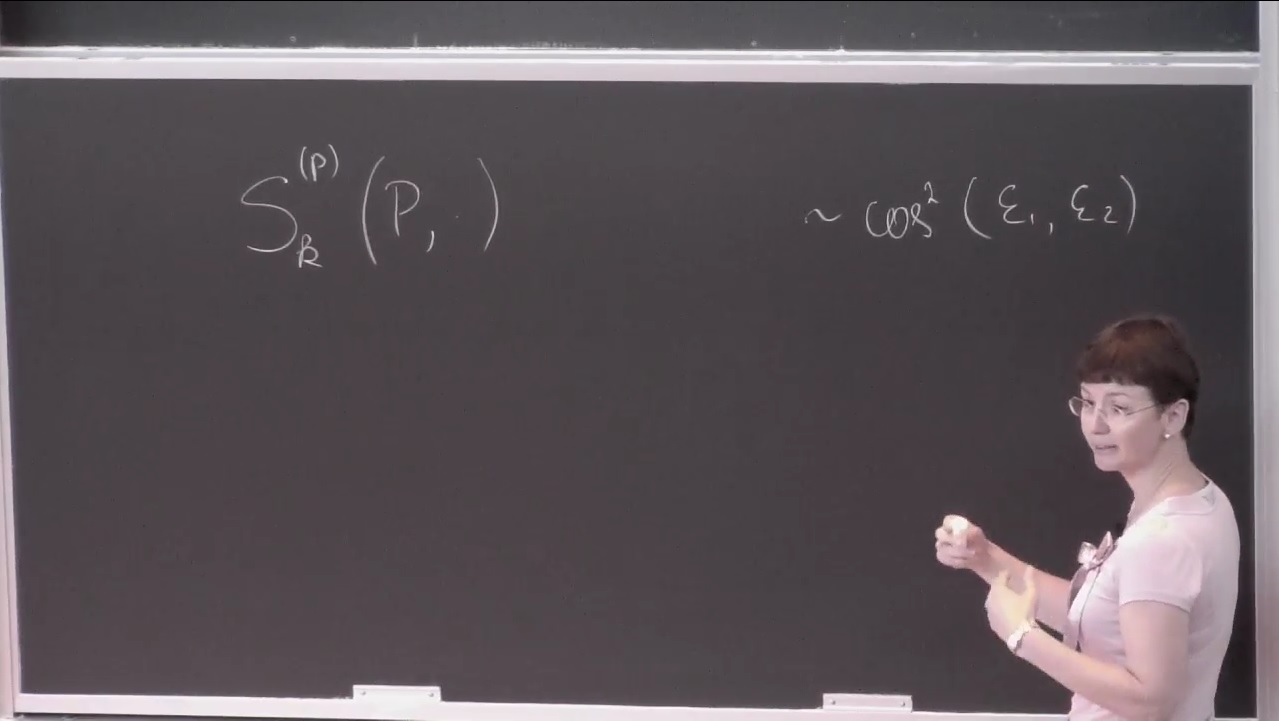Abstract
A flag area measure on a finite-dimensional Euclidean vector space is a continuous translation-invariant valuation with values in the space of signed measures on the flag manifold consisting of a unit vector v and a (p + 1)-dimensional linear subspace containing v.
Using local parallel sets, Hinderer constructed examples of SO(n)-covariant flag area measures. There is an explicit formula for his flag area measures evaluated on polytopes, which involves the squared cosine of the angle between two subspaces.
We construct a more general space of SO(n)-covariant flag area measures, which satisfy a similar formula for polytopes, but with an arbitrary elementary symmetric polynomial in the squared cosines of the principal angles between two subspaces. Hinderer’s flag area measure correspond to the special case where the elementary symmetric polynomial is just the product.
We also provide a classification result in the spirit of Hadwiger’s theorem. We introduce a natural notion of smoothness and show that every smooth SO(n)-covariant flag area measure is a linear combination of the ones which we constructed.