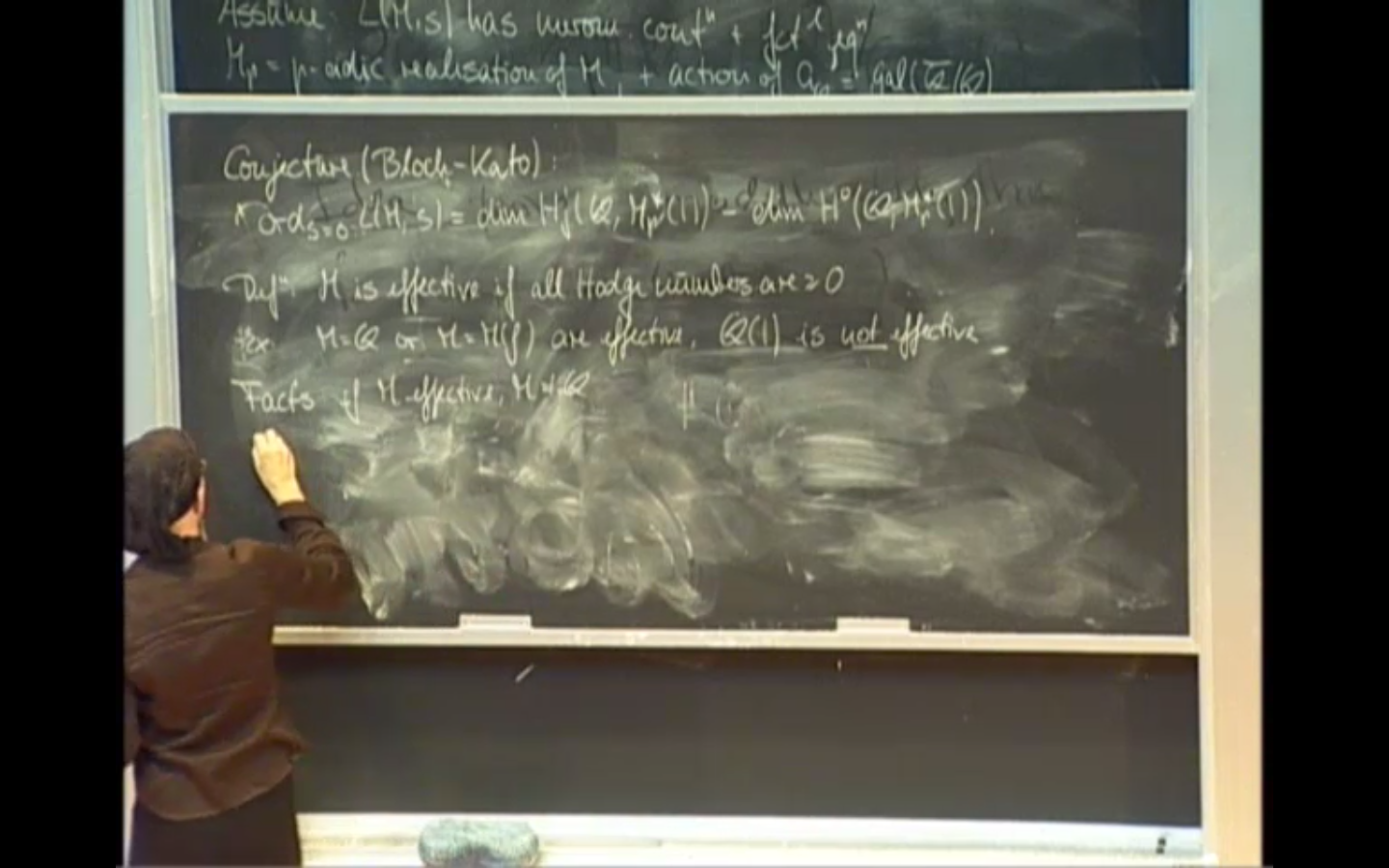I show how Beilinson's Eisenstein symbol give rise to motivic cohomology classes attached to pairs of modular forms of weight >= 2. These motivic cohomology classes can be used to construct an Euler system -- a compatible family of global cohomology classes -- attached to pairs of modular forms, related to the critical values of the corresponding Rankin-Selberg L-function. This is joint work with Kings and Loeffler, extending my previous work with Lei and Loeffler for weight 2 forms. This Euler system has several arithmetic applications, including one divisibility in the Iwasawa main conjecture for modular forms over imaginary quadratic fields, and cases of the finiteness of Tate--Shafarevich groups for elliptic curves twisted by dihedral Artin representations.