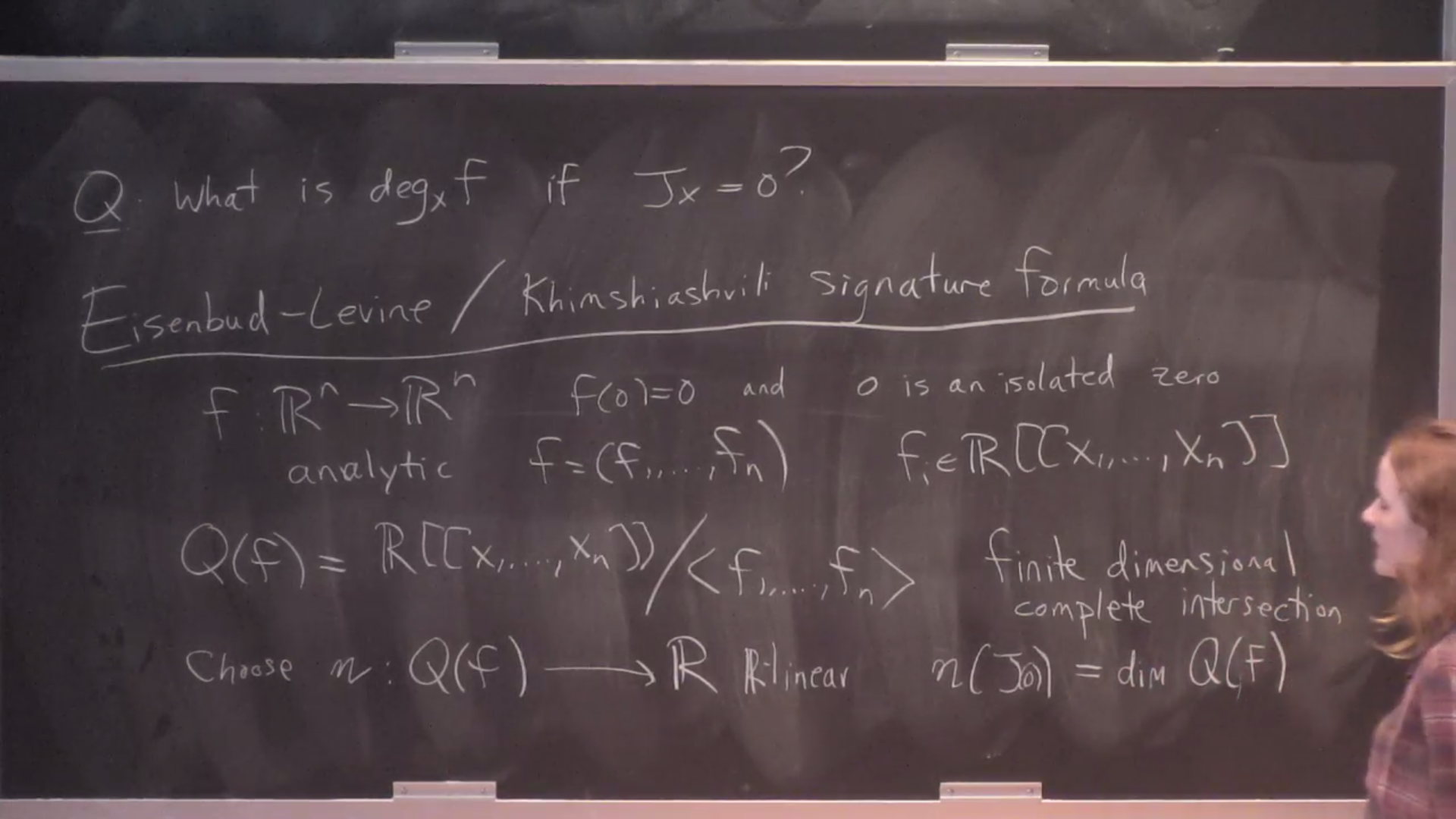Motivic Euler numbers and an arithmetic count of the lines on a cubic surface
Presenter
March 30, 2017
Keywords:
- Galois theory
- Galois orbits
- periods
- motivic integration
- Euler characteristics
- Cayley-Salmon theorem
- A1-homotopy theory
- Grothendieck-Witt group
- degree formulae
- Poincare-Hopf theorem
- enumerative geometry
- generalizations of classical theorems
- algebraic geometry
MSC:
- 11R34
- 11R32
- 11Rxx
- 11-xx
- 14-xx
- 14Cxx
- 14C30
- 55M25
- 55M20
- 55Mxx
- 55-xx
- 57R20
- 57R22
- 57Rxx
- 14Jxx
- 14J25
Abstract
A celebrated 19th century result of Cayley and Salmon is that a smooth cubic surface over the complex numbers contains exactly 27 lines. Over the real numbers, the number of lines depends on the surface, but Segre showed that a certain signed count is always 3. We extend this count to an arbitrary field using A1-homotopy theory: we define an Euler number in the Grothendieck-Witt group for a relatively oriented algebraic vector bundle as a sum of local degrees, and then generalize the count of lines to a cubic surface over an arbitrary field. This is joint work with Jesse Leo Kass.