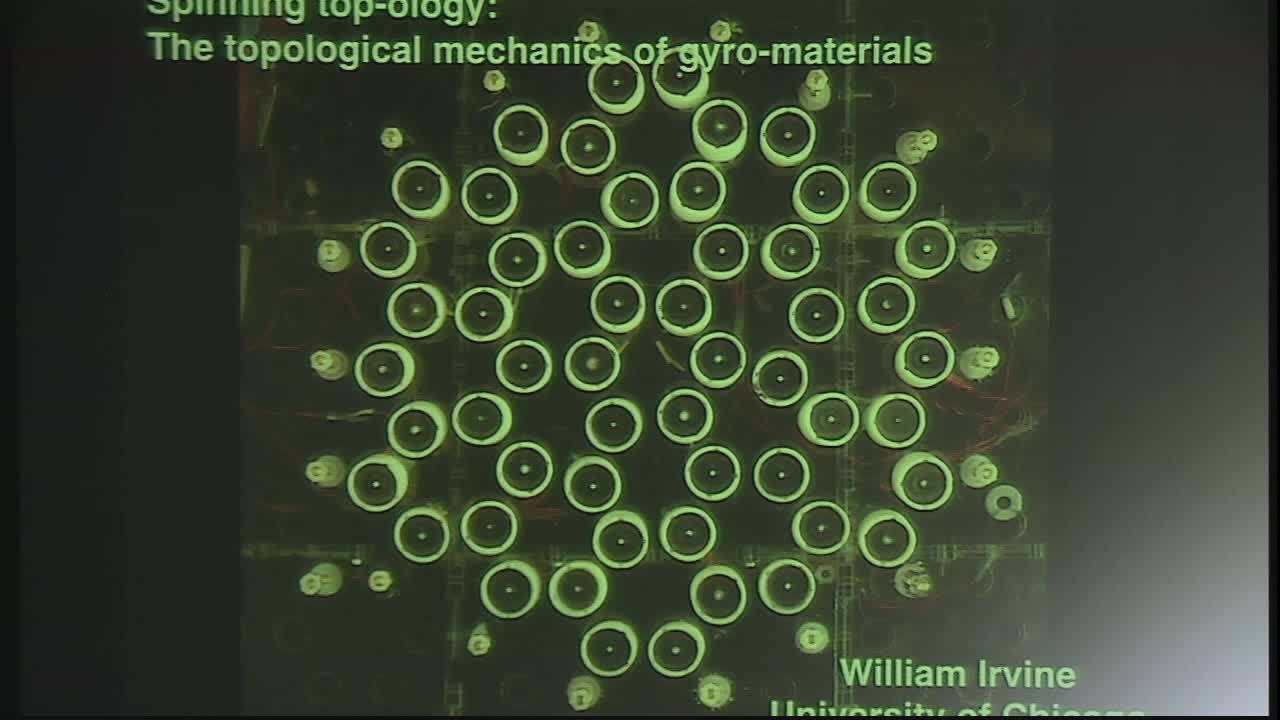
Spinning Topology in Ordered and Amorphous Mechanical Gyro-materials
Presenter
March 13, 2017
Abstract
Geometry and topology often play a powerful role in determining the organization and properties of materials. A recent example is the discovery that the excitation spectra of materials -- be they electronic, optical, or mechanical -- may be topologically non-trivial. This can have curious physical consequences, such as the formation of modes that are unusually robust to disorder.
I will discuss an experimental and theoretical study of a simple kind of active meta-material – comprised of coupled gyroscopes on a lattice – that naturally encodes non-trivial topology in its vibrational spectrum. These materials display a sonic gap populated by topologically protected edge modes which propagate in only one direction and are unaffected by disorder. We observe these edge modes in experiment and verify their robustness to disorder and the insertion of obstacles.
Crucially, the geometry of the underlying lattice controls a symmetry that is essential to the non-trivial topology of the spectrum: time reversal symmetry. We exploit this to control the chirality of the edge modes by simply deforming the lattice. Moving beyond ordered lattices we show that gyroscopic networks naturally give rise to amorphous mechanical topological insulators constructed using arbitrary point sets, including hyperuniform, jammed, quasi-crystalline, and uniformly random arrangements. The topology of the vibrational spectrum can be controlled through simple, local decorations.