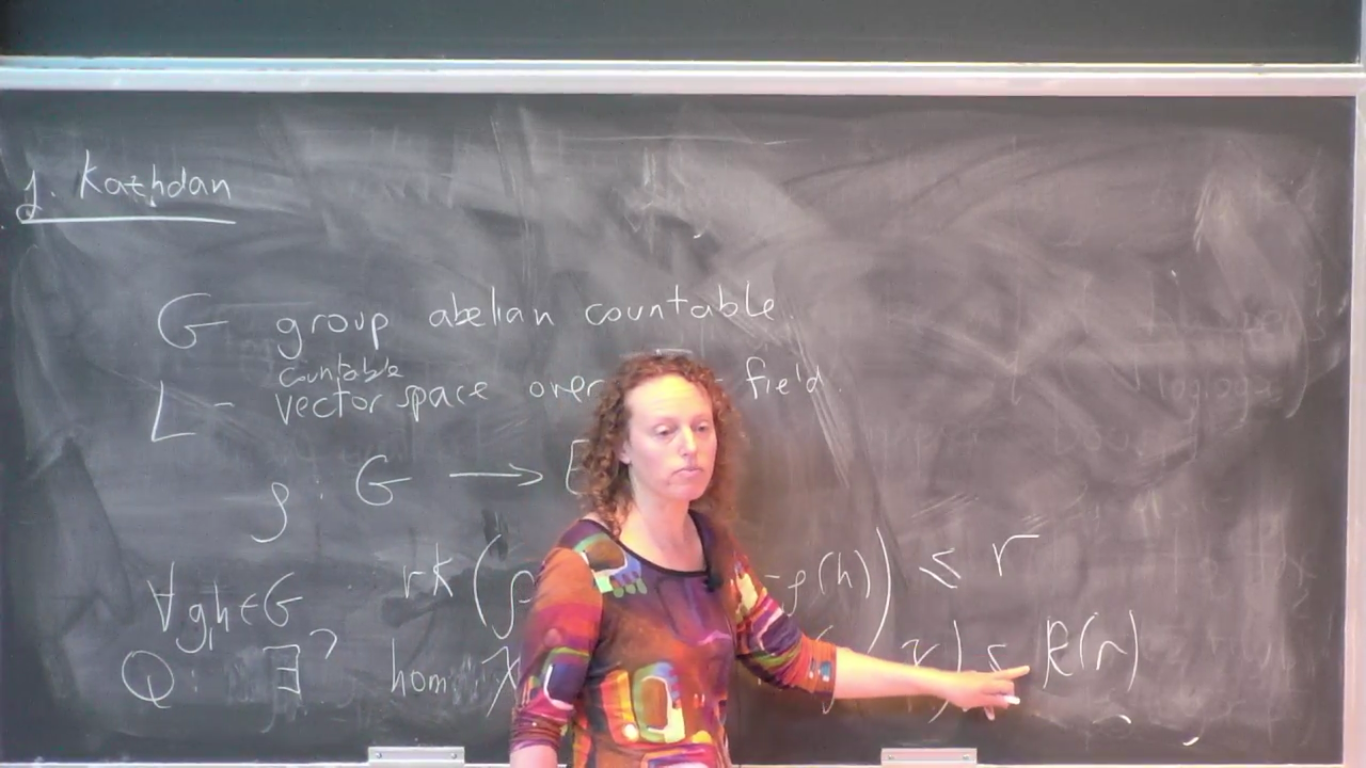Approximate cohomology
Presenter
May 1, 2017
Keywords:
- Gowers norm
- cohomology
- Fourier analysis
- inverse conjecture for Gowers norms
- homogeneous multilinear forms
MSC:
- 11F75
- 15A69
- 15A29
- 13D03
- 11T99
Abstract
Let V be an infinite vector space over a finite field k and let be an approximate homomorphism from V to End(V), i.e. the rank of f(x+y)-f(x)-f(y) is uniformly bounded by some constant r. We show that there is a homomorphism g such that f-g is of rank uniformly bounded by R(r).
We introduce a notion of a approximate cohomology groups and interpret this result as a computation of H^1 in a special case. Our proof uses the inverse theorem for the Gowers norms over finite fields; and an independent proof of this result (and some natural generalizations of it) would lead to a new proof of the inverse theorem. Joint work with D. Kazhdan