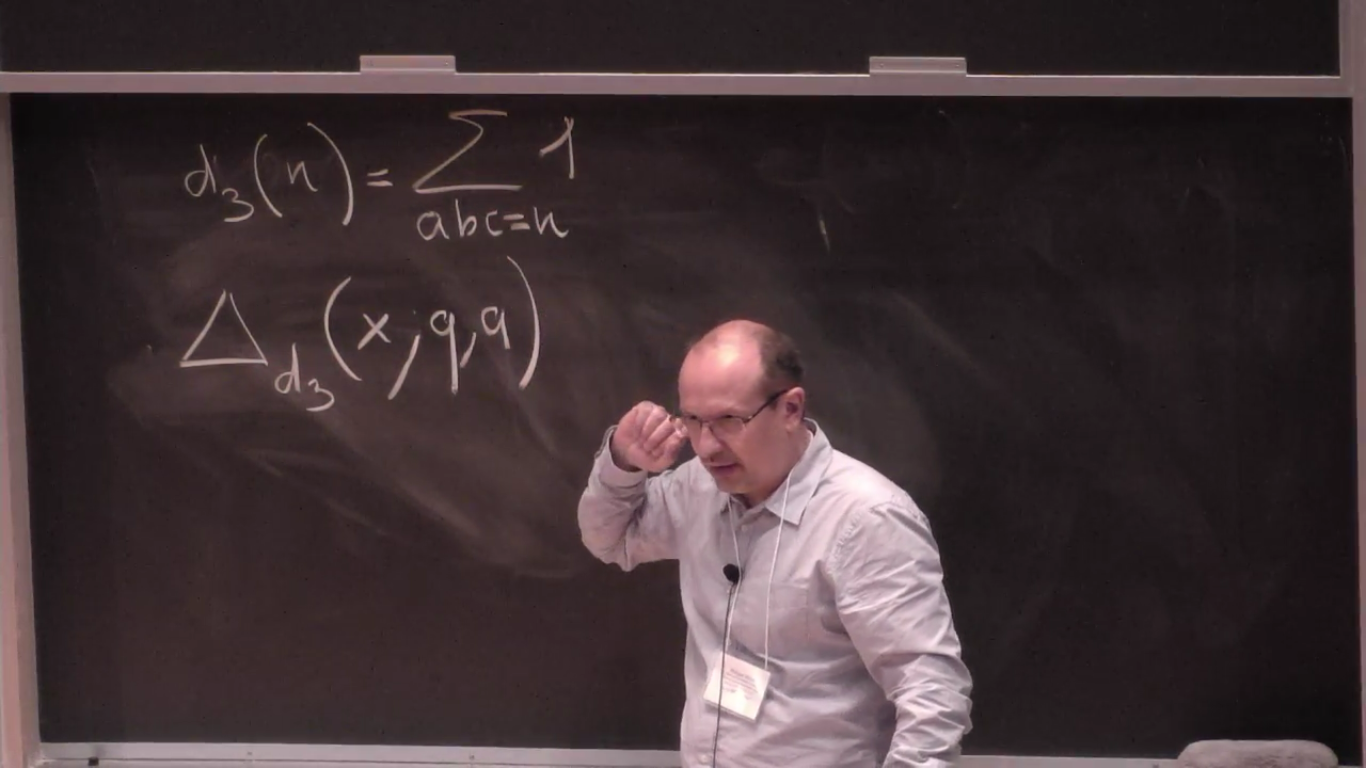Trace functions are arithmetic functions defined modulo $q$ (some prime number) obtained as Frobenius trace function of $\ell$-adic sheaves. The basic example is that of a Dirichlet character of modulus $q$ but there are many other examples of interest for instance (hyper)-Kloosterman sums. In this series of lectures we will explain how they arise in classical problems of analytic number theory and how (basi) methods from $\ell$-adic cohomology allow to extract a lot out of them. Most of these lectures are based on works of E. Fouvry, E. Kowalski, myself and W. Sawin.