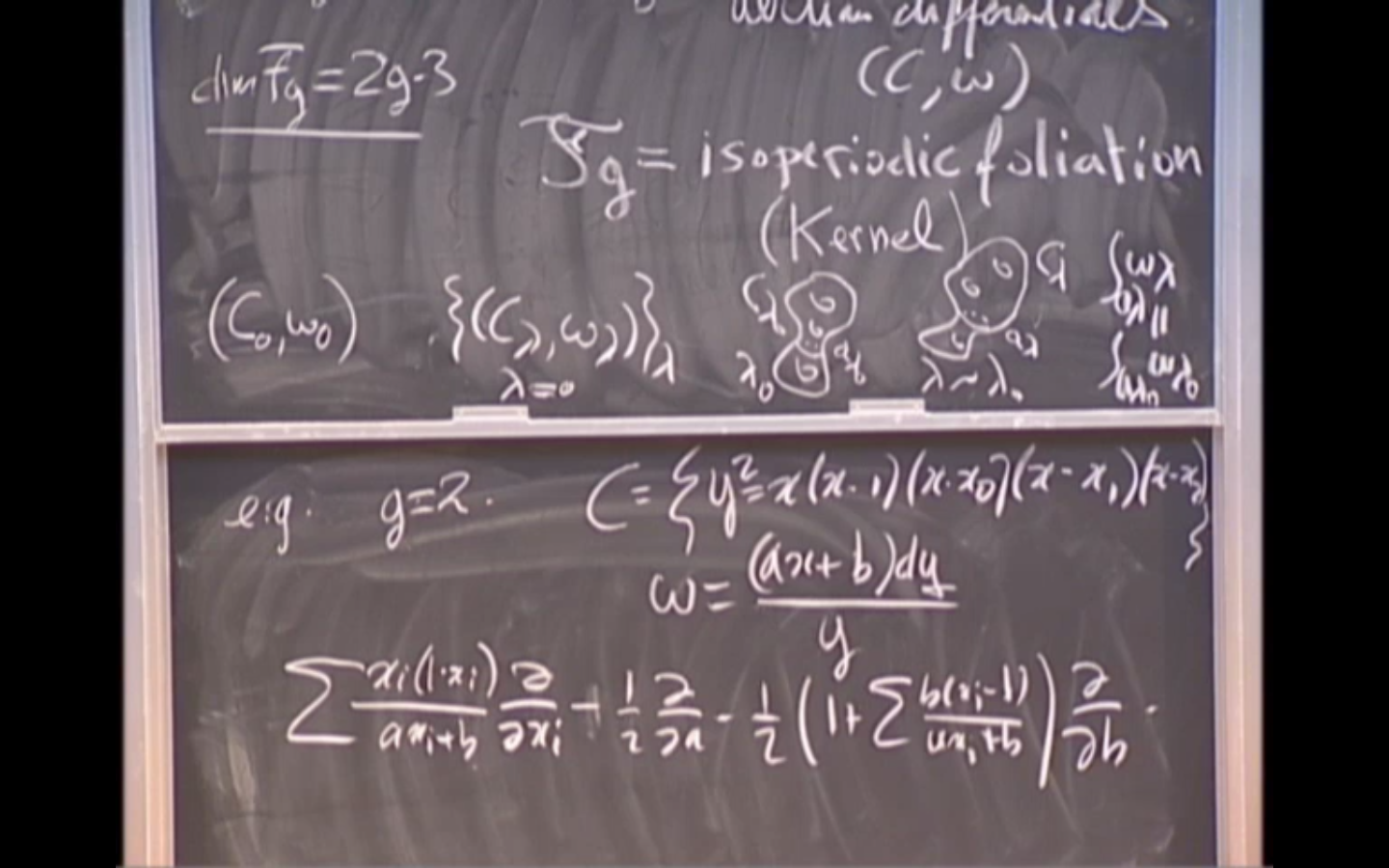Schiffer variations produce isoperiodic deformations on the moduli space of abelian differentials on algebraic curves of genus g, and define there an interesting algebraic foliations. I'll explain that the dynamics of this latter can be understood through the dynamics of the lattice Sp(2g,Z) on the homogeneous space Sp(2g,R)/Sp(2g-2,R). This transfer principle is based on a topological property of the period map (its fibers are connected). The fact that this property holds answers a question of McMullen, and generalizes a previous work of Simpson. This is a joined work with Calsamiglia and Francaviglia.