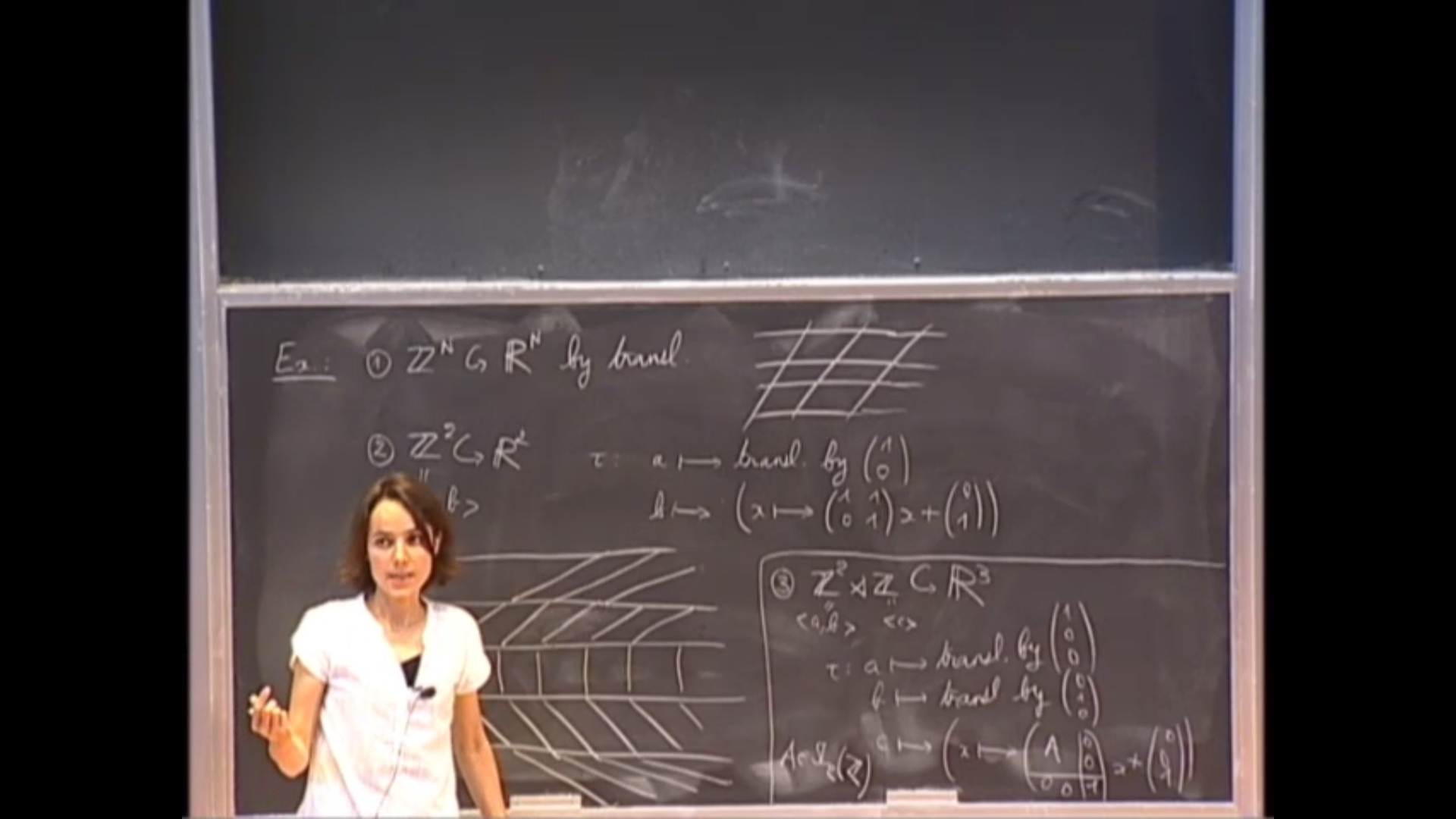Proper affine actions of right-angled Coxeter groups
Presenter
August 25, 2016
Keywords:
- geometric group theory
- hyperbolic group
- Coxeter groups
- Auslander conjecture
- affine buildings and cells
- affine geometry
- Lie groups
- O(p,q)
- quadratic forms
MSC:
- 20F65
- 20F67
- 20F05
- 20Fxx
- 20-xx
- 20F55
- 20F40
- 20F38
Abstract
The Auslander Conjecture states that all discrete groups acting properly and cocompactly on R^n by affine transformations should be virtually solvable. In 1983, Margulis constructed the first examples of proper (but not cocompact) affine actions of nonabelian free groups. It seems that until now all known examples of irreducible proper affine actions were by virtually solvable or virtually free groups. I will explain that any right-angled Coxeter group on k generators admits a proper affine action on R^{k(k-1)/2}. This is joint work with J. Danciger and F. Guéritaud.