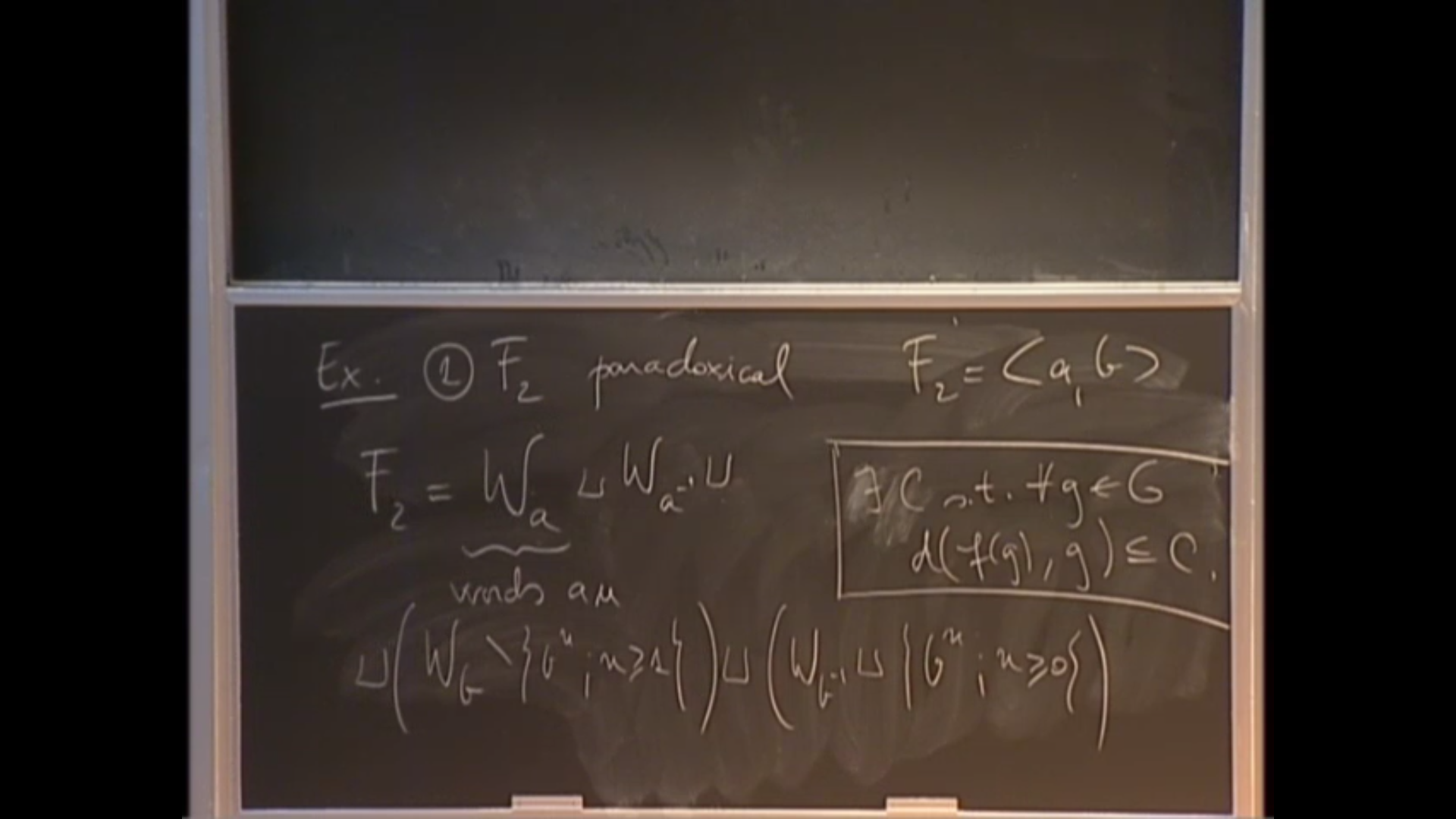Amenability and fixed point properties
Presenter
August 25, 2016
Keywords:
- geometric group theory
- hyperbolic group
- amenable groups
- Kazhdan's property T
- negative curvature manifolds
- Banach space
- expander graph
- mapping class groups
- von Neumann-Day conjecture
MSC:
- 20F65
- 20F67
- 20F05
- 20F06
- 20Fxx
- 20-xx
- 43A07
- 37F15
- 37F30
- 37Fxx
Abstract
A fundamental dichotomy in the theory of infinite groups is the one between amenable groups and groups with Kazhdan's Property (T). In this talk I shall overview versions of these two opposite properties, connections to actions on non-positively curved spaces and on Banach spaces, to other geometric features of the groups, and to expander graphs. I shall also mention what is known in the setting of random groups and that of important classes of infinite groups (e.g. lattices, mapping class groups, Out(F_n) etc).