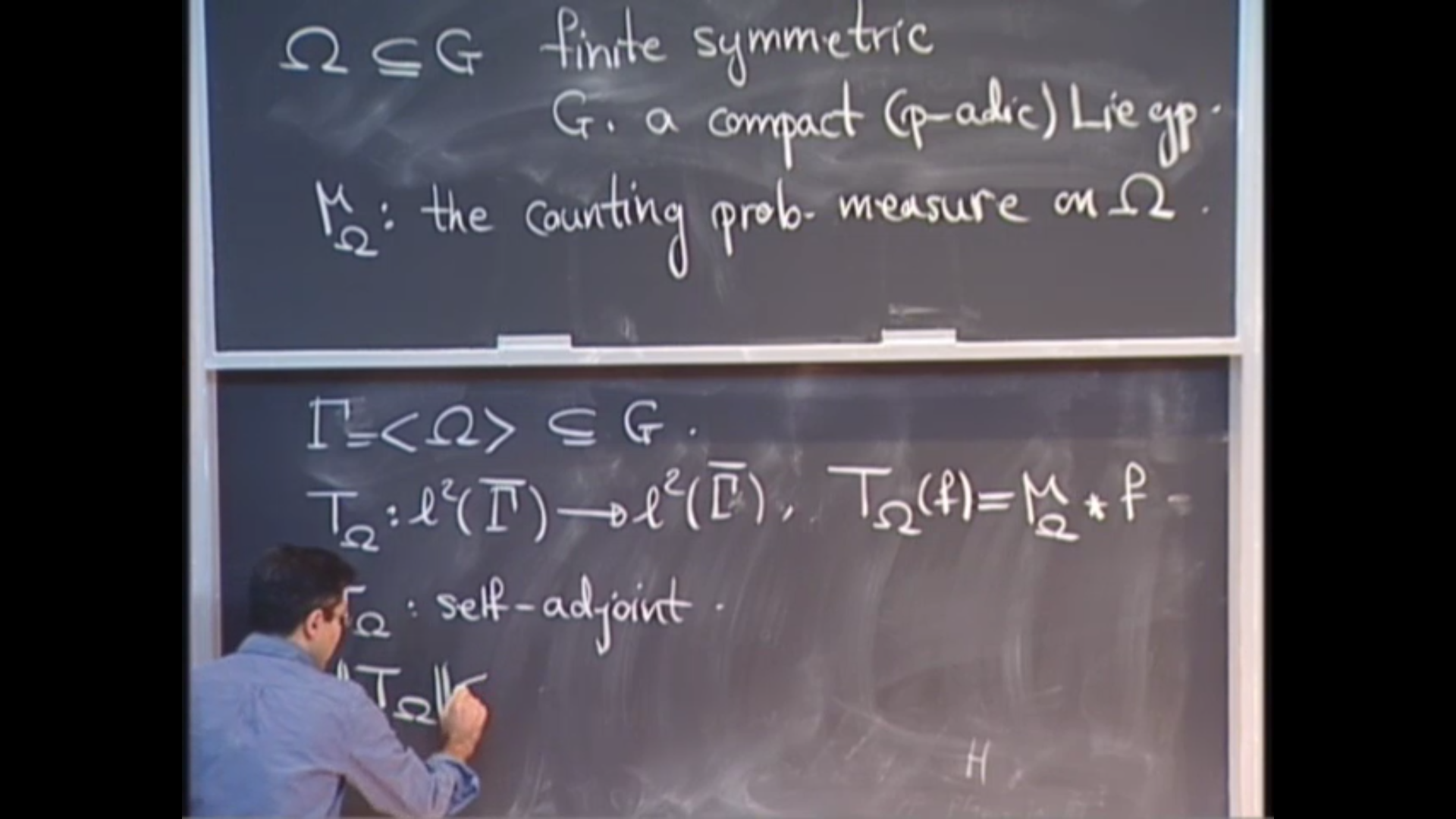Local spectral gap
Presenter
May 11, 2015
Keywords:
- Kazhdan's property T
- locally compact groups
- discrete subgroups
- random walks
- discrete group actions
- compact Lie group
- p-adic Lie group
MSC:
- 22Exx
- 22E05
- 22-XX
- 22E35
- 22E40
- 22Fxx
- 22F10
Abstract
(Joint with R. Boutonnet, A. Ioana) The notion of local spectral gap for general measure preserving actions will be defined. We prove that the left translation action of a dense subgroup of a simple Lie group has local spectral gap if the subgroup has algebraic entries. This extends to the non-compact setting recent works of Bourgain-Gamburd and Benoist-de Saxce. We also extend Bourgain-Yehudayoff’s result. The application of this result to Banach-Ruziewicz problem, delayed random-walk, and monotone expanders will be explained.