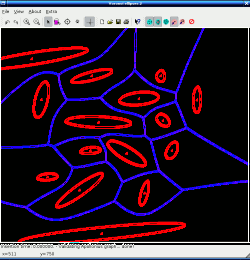
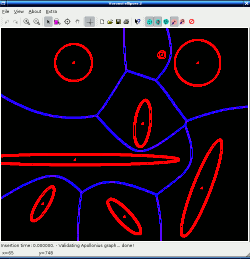
Innumerable scientific and engineering applications from geology to telecommunications lead to the same problem: given a set of objects, find which object is nearest to any particular point. The Voronoi diagram answers this question for every point on the plane by dividing the plane into cells containing the points nearest each object. Because this question arises in so many applications, highly efficient algorithms and codes for computing Voronoi diagrams have been developed in the case the objects are idealized as simple points. I. Emiris and E. Tsigaridas of the National University of Athens visited the IMA during the 2006-2007 program on Algebraic Geometry and focused on the problem of extending efficient algorithms for computing exact Voronoi diagrams to the case of more general objects which can be described algebraically, such as ellipses.

The hardest module to extend was something called the InCircle predicate, which decides the relative position of a query ellipse with respect to a circle externally tangent to three other ellipses. Emiris, Tsigarides, and Ph.D. student G. Tzoumas reduced this query to calculations on algebraic numbers of degree 184. To make these calculations rapidly, they figured out an approach combining certified numerical algorithms with algebraic computations.

The work of Emiris, Tsigarides, and Tzoumas provides the first complete implementation for the exact computation of the Voronoi diagram of ellipses. It is targeted for inclusion in the open source computational geometry library, CGAL , and so will join the toolbox available to mathematicians and scientists.

Related material

• Voronoi diagram of ellipses , the project website
• I. Emiris and G. Tzoumas, The Voronoi circle of smooth closed curves , poster for an IMA meeting 2007
• I. Emiris and G. Tzoumas, A real-time and exact implementation of the predicates for the Voronoi diagram of parametric ellipses , in SPM’07 , Beijing, China, June 2007
• I. Emiris, E. Tsigaridas, and G. Tzoumas, The predicates for the Voronoi diagram of ellipses , in SoCG’06 , Sedona, Arizona, June 2006