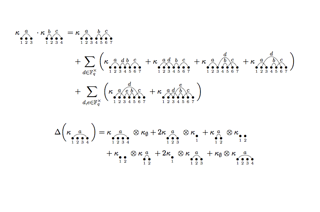The AIM workshop “Supercharacters and combinatorial Hopf algebras,” which took place in May 2010, solved one of the open problems in supercharacter theory and resulted in a paper authored by all 28 of the workshop participants.

The character theory of p-groups, such as U(n), the group of n x n uppertriangular matrices with coefficients in a finite field Fq (and ones on the diagonal) is a notorious difficult theory despite years of work. In fact, for U(n) it is not even known whether the number of conjugacy classes is a polynomial in q. In recent years a cruder version of a character theory, known as a `supercharacter theory,’ has been developed. This theory lumps together certain conjugacy classes and certain irreducible characters to yield a tractable theory that is still rich enough to solve problems. This coarser theory was first developed by Carlos Andre to study U(n) and it turned out to be rich enough that Arias, Castro, Diaconis and Stanley were able to use it to study a family of random walks. Supercharacter theory was then abstracted by Diaconis and Isaacs to arbitrary finite groups, and is currently in active development.

The organizers of the workshop believed that it was highly likely that the supercharacter theory of U(n) was in some sort of duality with one of the noncommutative symmetric function theories. In fact, it is known that there is an algebra isomorphism between the supercharacters of U(n) and the ring of symmetric functions in noncommutating variables; however, a canonical isomorphism remained elusive. It was also known that the combinatorics of characters of the symmetric group and the general linear group over a finite field have useful interpretations via a Hopf algebraic structure on the representations. Meanwhile, there has been great interest in the Hopf structure of various versions of non- commutative symmetric functions.

Thus, as Persi Diaconis said in his opening remarks at the workshop, the organizers thought an AIM workshop was just the right place to bring together experts in supercharacter theory and experts in combinatorial Hopf algebras and try to collaborate make progress on this most difficult problem.

In keeping with the AIM style of focused problems, the organizers decided first to tackle the following: Is there a Hopf algebraic connection between the Hopf algebra of symmetric functions in non-commuting variables and the ring of supercharacters of the unipotent upper- triangular matrix groups over a finite field with two elements?

To facilitate progress on the first morning of the workshop there were two survey talks, one an introduction to supercharacters with an emphasis on the case of unipotent upper-triangular matrices, and one an introduction to combinatorial Hopf algebras with an emphasis on the Hopf algebra of symmetric functions in non-commuting variables. The first afternoon was spent in small groups addressing the confusions of the morning.

The second morning’s talks gave some additional background material. The afternoon was dedicated to actually begin understanding the combinatorial underpinnings of the two structures we were studying, and, to the surprise of everyone, an answer was found to the problem in the course of the afternoon discussions.

With that success, the organizers decided to broaden the scope. By the end of the week, they had established a Hopf algebra isomorphism between the ring of supercharacters of the unipotent upper-triangular matrix groups over an arbitrary finite field and a Hopf algebra of symmetric functions in colored non-commuting variables and a symmetric function realization for the Hopf algebra dual space of the ring of super- characters of the unipotent upper-triangular matrix groups over an arbitrary finite field. The identification of these two different structures suggests a rich class of examples to investigate in future work in the emerging field of combinatorial Hopf algebras.

In addition, at the workshop an implementation of the underlying mathematics was implemented on a computer and is freely available on the web.

The ultimate goal at an AIM workshop is to everyone take part in some successful collaboration and this was resoundingly achieved at this workshop. All the participants are authors of a preprint, “Supercharacters, symmetric functions in non-commuting variables, and related Hopf algebras” (arXiv:1009.4134v1).