
Distinguishing Knots
An old question in mathematics is: how can we distinguish between knots? If we imagine a knot tied out of a piece of rope, the most basic problem is to tell if the knot can be “undone” by moving the rope around without breaking it. Although it may be difficult to see immediately, the following is an example of a knot which can be undone in this sense: i.e. the knot on the left can be transformed without breaking it into the “unknot” on the right:
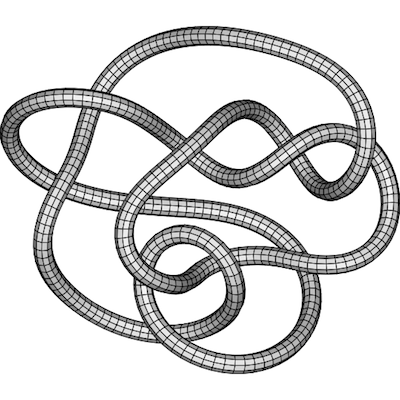
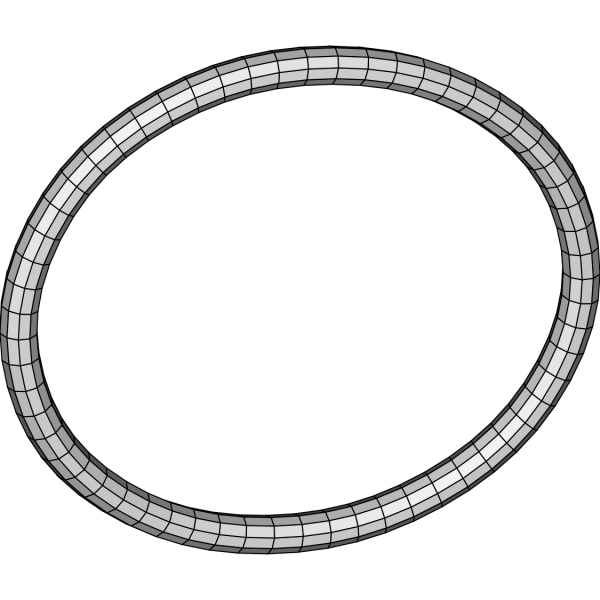
On the other hand, no amount of patient manipulation will transform
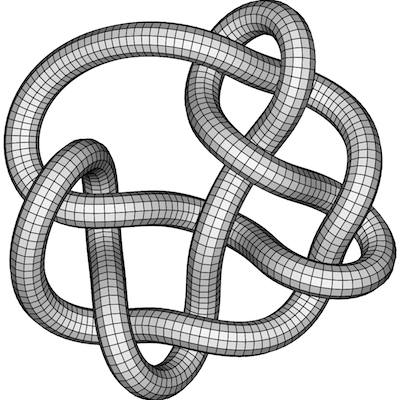
into the unknot. When presented with a complicated-looking knot, how can we tell whether it can be undone or not?
One way to approach this problem is the theory of matrix factorizations – one of the subjects of MSRI’s Spring 2013 scientific program. A polynomial is an expression of the form x2 + y2 + z2 in unknowns x, y, z. The polynomial x2 is the square of x, and while x2 + y2 is not the square of any polynomial there is a 2 × 2 matrix which squares to x2 + y2 times the identity matrix
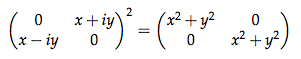
where i = √-1. Such “matrix square roots” of polynomials, called matrix factorizations, have been studied since the work of Eisenbud in the 1980s in connection with the geometry of hypersurface singularities. The set of all matrix factorizations of a polynomial, for example x3 + xy3 + z2, contains important geometric information about the singularity of the associated surface (the singularity is the “pinch point” in the following graphic):

It turns out that matrix factorizations are also relevant to the study of knots. By dividing a knot up into simple pieces, attaching to each of these pieces a matrix factorization, and combining together these matrix factorizations in a clever way, Khovanov and Rozansky construct an invariant of the knot. If we compute their invariant for two knots and get different answers, it is certain that no amount of manipulation can transform one knot into the other.
In this way techniques of commutative algebra can be used to study low-dimensional topology. Moreover numerous conjectures relate these invariants to symplectic geometry, representation theory, and BPS state counting in string theory. While it is too early to speculate about applications of Khovanov and Rozansky’s work in the real world, previous work in this area has been used in molecular biology and in one of the current approaches to constructing quantum computers using anyons.