Given a series of ordinary photographs of coffee mugs over a table, can you guess where the photographer was located at each shot? In other words, given  m central projections of piecewise smooth curves and surfaces, what are the translations and rotations of the underlying camera? The diagram below illustrates a case with  m = 3  where the goal is to recover two rotations and translations relative to the first camera, and then reconstruct the underlying geometry in 3-space. 

 Computer Science has had a surprisingly hard time solving this problem. While 3D computer vision has evolved to provide us with the technology behind such incredible advances as autonomous vehicles, strangely enough, when imaging simple, innocent-looking curves and surfaces appetizing to whimsical geometers and coffee aficionados alike, this technology fails miserably. This is because it relies on point patterns that correspond across the images, having to resort to devices such as laser projectors to artificially complexify smooth-looking objects with additional pattern. This indicates that a theoretical and technological breakthrough was needed to crack this problem. Award-winning research supported by ICERM has brought the algebraic geometry and computer vision communities together towards this effort. 

 The research revolved around strategic open problems originated from multiview differential geometry [MVDG16]. At first, the theory and a specialized solver for problems with a single camera using two curve points were completed, yielding a 16-degree algebraic system on 6 unknowns for the translation and rotation relative to an object [CPDG20]. But scaling this approach to more cameras was beyond the reach of hand-crafting solvers and generic symbolic technology rooted on Gröbner bases. To leverage curve geometry to compute relative camera configurations required at least three views [MVDG16], leading to more than a 10-fold increase in the algebraic degree. Such problems lie at the frontier between the tractable and intractable, between what can be computed robustly with global guarantees in feasible time, and what can only be tackled using local optimization sensitive to initial conditions. 

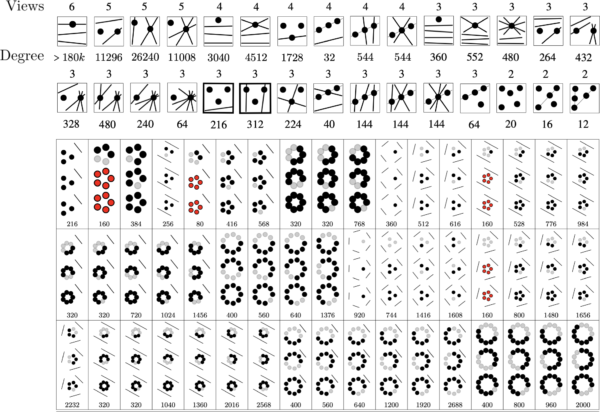
 From three corresponding points in three views, as in the above images, we discovered that, when at least two of the points lie on curves (ie, have a tangent direction, top row of the above figure), the algebraic equations yield 312 complex solutions, each corresponding to a camera configuration [TRPLP20]. Of these, on average 35 are real and 7 correspond to physical solutions. We leveraged cutting-edge numerical algebraic geometry based on a recent monodromy approach for homotopy continuation (above figure, right) to build the first solver for such high degree systems, that can run at the milisecond scale. The team generalized the analysis and toolset to a series of other fundamental problems. In a prize-winning paper [PLMP19], a rigorous classification using birational geometry, commutative algebra and combinatorics discovered all the 30 minimal problems mixing points and straight lines that exist in  m views, as well as their degrees, shown in the first two rows below. The 5th square on the second row, for instance, indicates that three points and a free line corresponding in three views are necessary and sufficient, and that the algebraic degree is 216. The same solver framework devised for the initial 312-degree problem works for the majority of these problems. This was further extended [PL1P20] to partial visibility in three views: when points and lines not all show up in all images. Minimal problems of practical interest in this case form an extensive zoo of 74575 equivalence classes, of which only 76 were known. The bottom table shows the 51 trifocal representative problems without considering lines incident to points and their respective degrees. Points not visible in a given view are indicated in grey. 

 A long-term question is: to what extent can the modern tools of algebraic geometry help solve 3D computer vision problems in a tractable way? Ongoing research directions include proving the impossibility of more efficient reformulations via Galois groups; integrating solutions along curves and surfaces; solving differential motion problems (video); manifold learning solution path geometry towards faster solvers; and higher order geometry beyond straight lines such as circles and cubics to model curvature and torsion. Our advances so far have delivered an impact to the field of Computer Vision, bridging modern theory and practice from algebraic geometry and its burgeoning Nonlinear Algebra community to solve geometric problems of great practical interest. This research also opens up many ways in which mathematics itself can be pushed to further solve hard problems, and for a greater understanding of geometry in general. 

 [MVDG16] Multiview Differential Geometry of Curves, R. Fabbri and B. Kimia, International Journal of Computer Vision (IJCV), 2016. 

 [CPDG20] Camera Pose Estimation Using First-Order Curve Differential Geometry, R. Fabbri, Peter J. Giblin and B. Kimia, IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI) (initial version appeared at ECCV’12), 2020. 

 [TRPLP20] Trifocal Relative Pose from Lines at Points. R. Fabbri, T. Duff, H. Fan, M. Regan, D. de Pinho, E. Tsigaridas, C. Wrampler, J. Hauenstein, P. Giblin, B. Kimia, A. Leykin and T. Pajdla, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022 (initial version appeared at CVPR 2020) https://arxiv.org/abs/1903.09755

 [PLMP19] PLMP – Point-Line Minimal Problems in Complete Multi-View Visibility, T. Duff, K. Kohn, A. Leykin, and T. Pajdla, IEEE International Conference on Computer Vision, 2019. (best paper award)  https://arxiv.org/abs/1903.10008 

 [PL1P20] PL1P – Point-line Minimal Problems under Partial Visibility in Three Views, T. Duff, K. Kohn, A. Leykin, and T. Pajdla, Arxiv, March 2020.  https://arxiv.org/abs/2003.05015 

[GMG21] Galois/monodromy groups for decomposing minimal problems in 3D reconstruction, T. Duff, V. Korotynskiy, T. Pajdla and M. Regan, SIAM Journal on Applied Algebra and Geometry, vol 6, Iss. 4, 2022. https://arxiv.org/abs/2105.04460

 Reported by Ricardo Fabbri (Rio de Janeiro State University), organizer of the Computer Vision Working Group of ICERM’s Fall 2018 Nonlinear Algebra semester program and the Winter  2019 Algebraic Vision research cluster .