When viewed from the outside, a human brain appears as a volume with a highly wrinkled surface having numerous long crevices. Sulcal fundi are 3D curves that lie in the depths of the cerebral cortex; informally, the fundus of a sulcus is the curve of maximal average depth that spans the length of the sulcus. The sulcal fundi serve as anatomical landmarks, `segmenting’ the cortex into functionally distinct regions. They are often used as landmarks for downstream computations in brain imaging and can be used in creating deformation fields for warping the cortical surfaces of different brains onto one another.

The notion of shape is a complex and somewhat nebulous concept. Topology is the mathematical subject that permits us to precisely measure and represent (in compressed fashion) shapes, both for standard notions of shape in two and three dimensions and for analogues in much higher dimensions.

One form of this measurement of shape comes through a sophisticated form of counting occurrences of patterns in shapes, called homology theory. One thing which can be extracted from homology theory is a collection of integers bk , called the Betti numbers, one for every non-negative number k, which perform counts of features such as loops in the shape. For instance, the first Betti number measures the presence of loops in a shape, so that the first Betti number of a capital letter A would be 1, and the first Betti number of a capital letter B would be 2. Note that this provides a robust way of distinguishing between these two letters, in the sense that these features are independent of the choice of fonts for the letter and of the angle at which the letters are viewed.

A striking development over the last 10-15 years has been the extension of this methodology (via a method called persistent homology) from completely specified shapes to shapes that are only known by some finite sample from them. These samples are called point clouds. In this case, we must replace the Betti numbers by more sensitive objects called persistence barcodes, which are just finite collection of intervals. The picture below illustrates a simple such situation.

The sampled object has a round, loop-like shape, and the barcode signals the presence of the loop via the presence of a long segment. The shorter segments are thought of as representing noise. If there were two loops in the point cloud, then we would see two long bars in the barcode.

This method can be used to study the shape of various kinds of objects coming up in science. One such example arises in the study of evolution, and has been described in the papers [1], [2]. One often thinks of the process of evolution as producing the so-called tree of life [3], with organisms, past and present, making up a shape in which nodes corresponding to particular organisms split into two or more descendants.

This kind of structure corresponds to clonal evolution, but when other forms of evolution, such as horizontal gene transfer, are involved, the structure of the point clouds are not tree like, but actually include loops. It is shown in [2] that one can often detect loops in data sets coming from viral evolution, and that they represent non-clonal evolutionary events. This appears to be only the starting point for the study of evolution using these methods. Numerous other applications of persistent homology have been developed, and are described in [1].

The figure below shows persistence barcodes and accompanying complexes for two different viral evolution situations, one with clonal evolution and the other with a non-clonal mechanism.

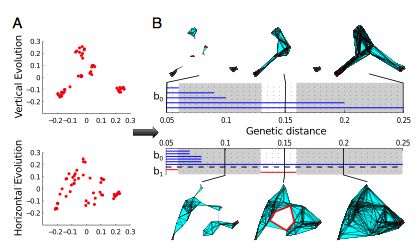
[1] G. Carlsson, Topological pattern recognition for point cloud data, Acta Numerica 23 (2014), 289-368.

[2] J. Chan, G. Carlsson, and R. Rabadan, Topology of viral evolution, Proc. Natl. Acad. Sci. USA 110 (2013), no. 46, 18566-18571.

[3] F. Delsuc, H. Brinkmann, and H. Philippe. Phylogenomics and the reconstruction of the tree of life, Nature Reviews Genetics 6.5 (2005): 361-375.