At a yearlong program at MBI, mathematicians, engineers, and bioscientists discussed new ways of analyzing the effects of random events on the long term behavior of large biological systems. A particular topic of interest was the development of stochastic methods in the study of infectious diseases. Within an individual, disease development involves both the stochastic evolution of viral or bacterial particles and the stochastic interactions between the particles and the immune system. And, on the population level, the contacts between individuals, and therefore the spread of the disease, have a large stochastic component. To make predictions that can guide public policy, stochastic issues must be studied at both levels, individual and population, and new mathematical methods must be developed to bridge the gap between the two scales.

The modeling approach of Kermack and McKendrick (1927) that divides the population into three groups (susceptibles, infected, and removed – the so-called SIR model) has been used historically as an important tool in deciding whether epidemics grow or dissipate. The SIR model uses the deterministic dynamics of ordinary differential equations (ODEs) to make its predictions in a number of different biological contexts, both on the micro-scale (for example, a viral infection of a host cell) and the macro-scale (for example, an infectious disease spread through a population). The ODE models have the advantage of simplicity, as they rely on the law of large numbers to longitudinally describe the average trends in a collection of molecules or viruses or other populations of interest. However, the dynamics of such collections are inherently stochastic phenomena and there are many reasons why one should use stochastic rather than ODE modeling to capture their dynamics.

On the micro scale (say for viral infections) the infection is typically initiated when a single cell of a viral template infiltrates the cell’s membrane. The key question at the initial stage is whether the virus will be able to reproduce itself in a sufficient amount so as to lyse the cell and move from an intra-cellular to an inter-cellular stage of infection. Often the initial model of viral reproduction may be approximated by a branching process. The approximation is possible due to the fact that in early stages of an infection the few viral particles are spatially separated and act, in essence, independently of each other. The branching approximation allows one, for instance, to obtain statistical procedures for estimating, given some current observables of the infection process, what the probability of a successful infection may be. On the other hand, once the virus establishes itself in the intra-cellular environment after lysis, the dynamics of an infection changes, due to triggered interaction with the immune system as well as with the local tissue structure.

On the macro scale, the need to account for spatial and temporal effects of a disease outbreak is one of the major reasons for moving away from the traditional ODE models which assume a well-mixed or homogenous population environment. Instead, such ODEs need to be replaced with more detailed models capable of tracking infections in multiple heterogeneous environments and of accounting for the complicated topology of modern travel and migration patterns, animal production activities, and relevant social and economic structures. Whereas the need for more accurate predictions of the viral behavior is of obvious interest in immunology and pharmacology, the need for more realistic modeling of the epidemic process is also becoming increasingly apparent as a pressing public policy issue. Especially, since the financial consequences of infectious disease outbreaks are increasingly burdensome on a global scale. Three important recent examples are the 2001 foot and mouth disease (FMD) outbreak in the UK (which was both widespread and deadly), the severe acute respiratory syndrome (SARS) epidemic in the spring of 2003 (which was deadly, but not as widespread as initially predicted), and the worldwide H1N1 (swine flu) pandemic of 2009 (which was widespread, but not nearly as deadly as initially feared).

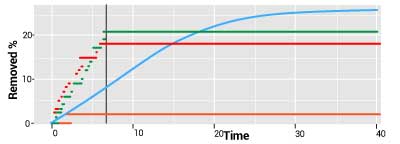The MBI stochastic program stimulated the scientific discussion about how stochastic techniques added to the traditional ODE models can improve the accuracy of model-based predictions. The SIR threshold principle states that if the initial number of susceptible individuals exceeds a threshold that is computable in the models, then a major outbreak will occur. The stochastic version of this results states that the threshold principle is true only with a certain probability. Thus, in some cases in which the determinist model predicts an outbreak, there is in fact a substantial probability of having no outbreak at all, which is what seems to have been the case in H1N1. The principle is illustrated in the figure plots which depict a continuous deterministic (light blue) and three step-function stochastic trajectories of a cumulative infectives count in an outbreak model. The step functions reach their highest points sooner (the vertical line), implying that the infection is likely to die out earlier than predicted by the deterministic model. There is also a high probability of no outbreak (the orange curve).

Considering stochasticity in disease spread brings up multiple modeling challenges that require the enhancements of old as well as the development of new mathematical approaches. One of the several techniques explored during the annual program was the multi-scale approximation method that formalizes the notion of augmenting the ODE model with certain stochastic effects and was first proposed by Ball, Kurtz, Popovic and Rempala (2006). The method brings a unifying approach to modeling random phenomena spanning multiple time scales and orders of magnitude and as such shows particular promise in analyzing disease spread on both the micro and macro scales. For instance, multi-scale approximation allows one to simultaneously model the behavior of a viral infection both at the intra-cellular (for instance, via a branching process) and at the inter-cellular levels (for instance, via an ODE or a large volume diffusion approximation). It may be also used to improve the predictive power of stochastic epidemic models of the SIR type and to simplify the computational burden of the necessary numerical approximations in data-driven analysis.