In the Fall of 2013, ICERM had a semester program on experiental geometry, topology, and dynamics . One of the many projects undertaken during this semester was the study of polygon iterations – geometrically defined maps on the space of polygons.

Perhaps the simplest polygon iteration is the midpoint map. Starting with an n-gon P1, we let P2 be the n-gon whose vertices lie at the centers of the edges of P1. The construction can be done over and over again, producing a sequence {Pn} of polygons which shrink to a point. If these polygons are rescaled (and suitably rotated) so as to have unit diameter, then, for almost every choice, they converge to an affinely regular n-gon. That is, the limit has the form T(Rn), where T is an affine transformation and Rn is a regular polygon.

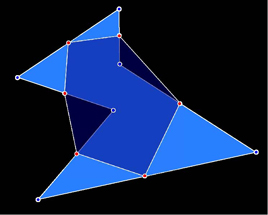
Figure 1: P1 is black and P2 = H(P1) is red.

The midpoint map is very close to the heat equation, in that the map averages out the coordinates of the polygon. The proof of the convergence properties of the midpoint map leads quickly into a discussion of finite Fourier series. Thought of as a map on Cn, the midpoint map is a linear map whose eigenvalues have the form

Ek = (1, ωk, ω2k, …, ωnk), ω = exp(2,πi/n).

Almost every point in Cn is attracted to a linear combination of E1 and E-1, the eigenvectors having the largest corresponding eigenvalues, and such linear combinations are affinely regular.

Figure 2 shows a more exotic example. One starts with the blue polygon P1 (in this case a pentagon) and then constructs the new yellow polygon P2. The rest of the picture is just scaffolding for the construction. Like the midpoint map, the vertices of P2 lie on the edges of P1. This map is even more symmetric than the midpoint map. If you pick up the paper and look at the picture in perspective, the midpoint map will not appear to be picking out the midpoints. However, the new map does the same thing from every perspective.

Figure 2: P1 is blue and P2 = H(P1) is yellow.

We call this map the projective heat map, because it shares some features of the midpoint map, but is natural with respect to the group of projective transformations of the projective plane. The projective heat map induces a map on the space Pn of projective equivalence classes of (not necessarily convex) n-gons in the projective plane. Unlike the midpoint map, the projective heat map is nonlinear; in general it is some rational map in 2n − 8 variables. The space Pn has a natural origin, the equivalence class of the regular n-gon, and computer experiments suggest that almost every point in Pn converges to the origin under iteration.

We were able to prove this result when n = 5. When n = 5, we get a rational map of the plane. We showed that the set J5 of pentagon classes which do not converge to the origin has area 0. The set J5 has an intricate fractal structure. Figure 3 shows a close-up of part of J5.

Figure 3: (Part of) the set J5.

The method of proof is to partition the plane into small polygons on which the action of the map is fairly easy to understand. The action of the map on these small polygons is then estimated by computer-aided manipulation of huge integer-valued polynomials.