In a well-shuffled deck of cards, about half of the pairs of cards are out of order. Mathematically, we say that in a permutation [math]$\pi$[/math] of [math]$[n]=\{1,2,\dots,n\}$[/math] there are about [math]$\frac12\binom{n}{2}$[/math] inversions, that is, pairs [math]$i<j$[/math] for which [math]$\pi(j)<\pi(i)$[/math].  Suppose we are interested in studying permutations for which the number of inversions is exceptionally large or small, for example [math]$\alpha\binom{n}{2}$[/math] for some other [math]$\alpha\in[0,1]$[/math]. What can one say about the structure and properties of such a permutation? For example, typically how many double inversions (triples [math]$i<j<k$[/math] for which [math]$\pi(k)<\pi(j)<\pi(i)$[/math]) might one expect?

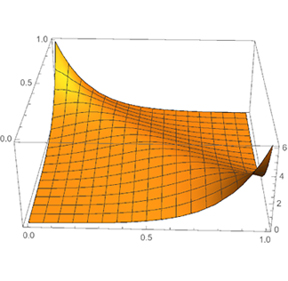
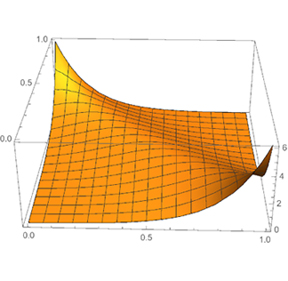
Figure 1: A permuton with density [math]$3/4$[/math] of inversions.

Figure 1 is an illustration of the shape of a large permutation with a fraction [math]$3/4$[/math] of inversions ([math]$\frac34\binom{n}{2}$[/math] total inversions), in a large-[math]$n$[/math] limit. What we are actually drawing is called a permuton: a probability measure on [math]$[0,1]^2$[/math] with uniform marginals (well, we’re graphing its probability density function). How does a permuton describe a large permutation? A permuton is, in a well-defined sense, the limit of the scaled permutation matrices associated to larger and larger permutations. The permutation matrix associated to a permutation of [math]$[n=300]$[/math] and [math]$3/4$[/math] fraction of inversions is shown in Figure 2.

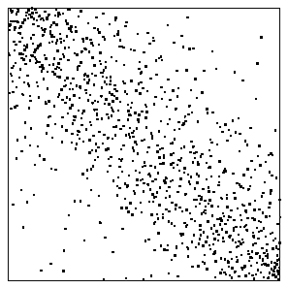
Figure 2: A permutation matrix of a uniform random permutation with density [math]$3/4$[/math] of inversions.

Generally a pattern in a permutation is an order-sequence imposed on a finite subset of [math]$[n]$[/math]; for instance, the permutation 34251 contains 5 copies of the pattern 231 (342, 341, 351, 451, and 251).  The density of a pattern [math]$\pi$[/math] of length [math]$k$[/math] in a permutation [math]$\sigma$[/math] on [math]$[n]$[/math] is the number of occurrences of the pattern [math]$\pi$[/math], divided by [math]$n \choose k$[/math].

If we fix the densities [math]$d_1,d_2 \ldots$[/math] of a few specific patterns, such as 12 and 123, the set of all permutations in [math]$S_n$[/math] with approximately those densities takes on a `bulk persona’, or limit shape. Most permutations in the set look alike; for example, their other pattern densities match.  Moreover, the limit shape, with
these constraints, varies smoothly (in fact analytically) except for an occasional singularity when a `phase boundary’ is crossed. This is why we can assert that
almost all permutations with density [math]$3/4$[/math] of inversions `look like’ Figure 1.

How do we find the permuton for a given set of densities? This can be realized with the recent derivation [Kenyon, Král’, Radin, Winkler: arxiv:1506.02340] of a variational principle. Starting from the fact that the number of permutations in [math]$S_n$[/math] with given constraints [math]$\bar%20d$[/math] is generally of the order [math]$n!\exp(sn)$[/math], the (negative) `entropy’ [math]$s=s(\bar%20d)$[/math], maximizing entropy allows one to find the permuton. That is, one can define an entropy function [math]$H$[/math] on the space [math]$\Gamma$[/math] of permutons and the desired permuton is obtained by maximizing [math]$H$[/math] over all permutons satisfying the given pattern constraints [math]$\bar%20d$[/math]:

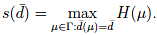
This gives a way to understand what a typical large, constrained permutation is like. If, as seems to be the usual case, there is a unique optimal permuton [math]$\tilde \mu$[/math] representing [math]$s(\bar%20d)$[/math], we can, via integration over [math]$\tilde\mu$[/math], obtain all other pattern densities of a typical large permutation with constraints [math]$\bar%20d$[/math]. This opens up a world of phases and phase transitions in a new setting.

This variational principle was an outgrowth of the Spring 2015 Phase Transitions and Emergent Properties program of the Institute for Computational and Experimental Research in Mathematics (ICERM).