ALEX WRIGHT AND KATHRYN MANN

Imagine that you are in a room with walls made out of mirrors. The room may be very oddly shaped and have corridors and nooks, but all the walls are at mirrored planes. If you light a single lamp, must every point in the room be illuminated? Perhaps surprisingly, the answer to this problem is “no”, and the reasons are connected with deep mathematical problems whose solution earned Maryam Mirzakhani the Fields medal in 2014.

One of the first examples of a room that is not illuminated at every point was given by Tokarsky, it has the floor plan below. When the light source is placed at either one of the red dots, the other will not be illuminated.

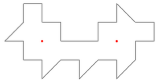
Very recently, Lelièvre, Monteil and Weiss showed that for a great many polygonal rooms, even very complicated ones, the behavior in Tokarsky’s example is the worst that can happen: no matter where you put the light source, all but a finite number of points in the room will be illuminated.

There are many related questions that can be answered by similar methods. One, called the security problem , considers an assassin with a laser who wants to shoot a target in a polygonal room where the laser beam can bounce off the walls. We now understand that the assassin has the advantage in this situation – in most rooms, it is not possible to block the target from the assassin with finitely many bodyguards, unless the target and assassin are in very particular positions.

The mathematical machinery behind the solutions to these problems involves a procedure of “unfolding” the polygonal room to give a surface where light rays travel in straight lines instead of bouncing. Below is a technical illustration of the unfolding of a square room; the crooked trajectory of light bouncing off the walls of the original bottom-left square becomes a series of straight lines, which the mathematician thinks of as a single straight line.

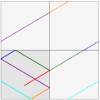
These “unfolded rooms” are called translation surfaces , and their typical behavior is studied by stretching and shearing them using matrix transformations. Mirzakhani’s recent Fields medal was awarded in part for her joint work with Alex Eskin and Amir Mohammadi on understanding the structure of the space of all shearings and stretchings of translation surfaces. These results originate in the subject of ergodic theory and dynamics on homogeneous spaces, the focus of the MSRI semester in Winter and Spring 2015.

The illumination and security problems also have surprising deep connections to algebraic geometry. For example, Bouw and Möoller used the theory of Variation of Hodge Structures to discover new examples of four sided polygons, such as the one pictured below, with the remarkable property that every laser beam in a mirrored room of this shaped will either repeat its path periodically, or equidistribute, filling evenly the whole room.

In contrast, there is a vexing array of possible behaviors for a laser beam in an arbitrary polygonal room; our understanding of these possible behaviors is an ongoing enterprise.

A central theme in mathematics is that good research, although possibly quite abstract, turns out to have applications and connections far beyond the original motivation for the research. In this case, ideas originally developed for abstract number theory have been applied to the seeming unrelated problems of illumination and security, and sophisticated results in algebraic geometry have given us new insight on light reflecting in polygons.

On the flipside, our efforts to understand the seemingly simple illumination and security problems have motivated the development of sophisticated new tools which in turn inform abstract research in number theory, algebraic geometry, and other fields.