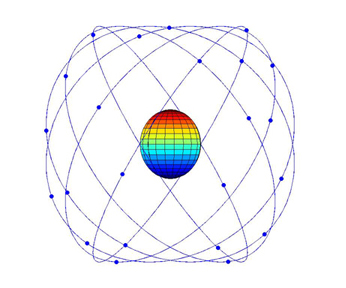The Global Positioning System (GPS) is global navigation system consisting of at least twenty-four satellites orbiting in six planes around the earth. GPS is extensively used by both the military and the FAA, with growing applications in civilian markets. The importance of GPS in everyday and military life continually increases with the development of smart phones and TomToms and the pressing need to track terrorists and drones and survey complex military missions.

Many users of GPS require an answer to the question: How accurate is the GPS constellation? A commercial airline pilot landing at Chicago O’Hare in a snowstorm would struggle if vertical measurement uncertainty were plus or minus ten meters – he might think the plane has landed when it’s ten meters above ground! Further, these uncertainty measurements are used to optimize GPS constellation measurement across the whole surface of the earth. “Optimizing” generally involves finding the optimal number and geometry of satellites in the sky, thereby minimizing measurement uncertainty.

Engineers at the Aerospace Corporation, a Federally Funded Research and Development Center headquartered in El Segundo, CA, manage the GPS constellation and require efficient and intuitive calculation of GPS performance metrics to perform these optimization problems. Positional Dilution of Precision (PDOP), one such performance metric, is defined as:

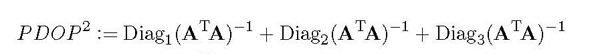
where A is a matrix with the unit vectors pointing up to the “m” satellites in view in its first three columns and ones in the fourth as scaled time. Taking satellite failures and other complications into account, optimization routines involve problems \( 10^{12} \) times larger than computing hundreds of thousands of 4×4 matrix inverses. This necessitates developing efficient and intuitive formulations for PDOP to be used in these expensive constellation optimization problems.

Paul Massatt and the Aerospace Corporation derived an efficient formulation for PDOP when there are four satellites in view (A is a square matrix), and the RIPS2010 team generalized this result to any number of satellites in view (A is in general a non-square matrix). The results were then generalized to support multiple Global Navigation Satellite Systems relying on different timing systems, programmed into Aerospace’s software and published in the Proceedings of the 2011 International Technical Meeting of The Institute of Navigation. The article can be found here.

Students David Puelz, Amber Richter, Aaron Mosher, and Matthew Kosko plus academic mentor Yana Landa
formed The Aerospace Corporation team at Research in Industrial Projects for Students (RIPS) Program, 2010.