A breakthrough in the sparse representation of data was made in the Fall of 2004 by David Donoho and by Emmanuel Candes and Terence Tao, in part at IPAM’s Multiscale Geometry and Analysis program. Their important results reduce a computationally difficult problem to an easily stated, convex minimization problem (the basis pursuit problem):
$$min|u{|}_1\text{such that}Au=f.$$

In this statement, $u$ is an unknown vector in ${\mathbb{R}}^n$ and $|u{|}_1=\sum _i|u_i|$ is its $L_1$ norm in ${\mathbb{R}}^n$, $f$ is a given vector in ${\mathbb{R}}^m$, $A$ is a short fat matrix with $m$ rows and $n$ columns in which $m<n$.

As stated in an earlier IPAM featured research highlight: “This body of work has had enormous impact”. One example is a recent multimillion dollar DARPA initiative to recover digital data from sparse measurements of analog signals.

Finding efficient methods to solve this convex basis pursuit optimization problem remained an important challenge. It cannot be solved efficiently by linear programming, if the matrix $A$ is large-scale and dense, and it was not known how to take advantage of available fast transforms for those $A$ taken from rows of orthonormal matrices.

In the Fall of 2003, Martin Burger and Stan Osher, together with Donald Goldfarb, Jinjun Xu and Wotao Yin, motivated by an IPAM Workshop on Inverse Problems in Imaging, realized that classical total variation ( $TV$ ) based image restoration could be greatly improved by an old technique called Bregman iteration, invented by L. Bregman in the 1960s for other purposes. Total variation involves the $L_1$ norm of the gradient, which turns out to be crucial for this method to be effective. Total variation minimization allows discontinuities, e.g. step like solutions, while $L_1$ minimization allows isolated spikes.

After several visits to IPAM by Yin, Goldfarb and Jerome Darbon during the spring of 2007, it became clear that Bregman iteration should be tried for the basis pursuit problem. This turns out to be the most effective way to solve the $L_1$ minimization problem [SIAM J. Imaging Sci., 1:143-168 (2008), DOI: 10.1137/070703983 ], yielding simple (in some cases, just two line) algorithms, which rapidly converge, effectively remove noise, and work for solutions which span 10 orders of magnitude. New algorithms (and theoretical justification) keep coming. T. Goldstein co-developed the split-Bregman method which rapidly solves total variation and other combinations of $L_1$ oriented problems. Emmanuel Candes and co-authors Jianfeng Cai and Zhowei Shen use the “two line” Bregman algorithm to solve the matrix fill in “Netflix” problem using the nuclear norm of a matrix. A UCLA group used $L_1$ minimization to effectively solve hyperspectral demixing for the National Geospatial Intelligence Agency (NGA).

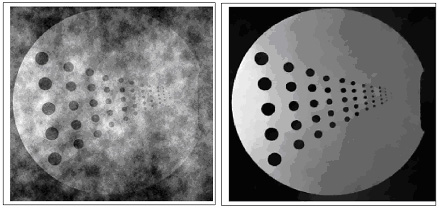
Additionally, the algorithm’s speed is expected to lead to many additional applications, e.g. real time restoration of an ultrasound video of a needle tip and rapid recovery of sparsely sampled MRI images, as in the picture below. The key fact is that this iterative procedure puts spikes/edges in the right locations almost immediately for $L_1/TV$ problems.

Magnetic Resonance Imaging of a sharp disk, using a traditional method (left) and a new method based on Compressed Sensing and Bregman iteration (right), from work of T. Goldstein.